七年级数学上：第三章字母表示数复习课件北师大版 课件VIP免费

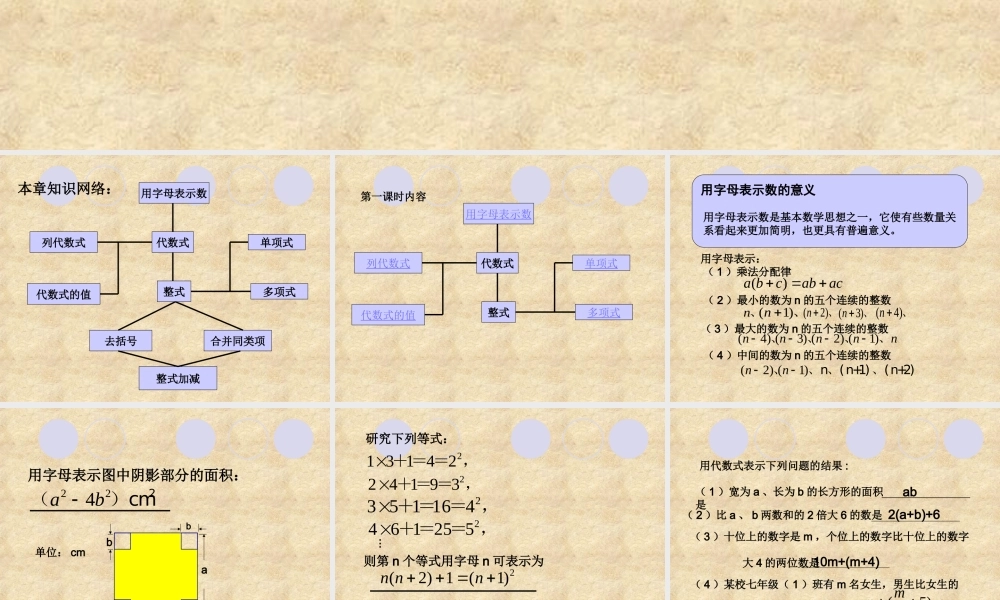
第三章字母表示数复习课 用字母表示数代数式整式单项式多项式列代数式代数式的值去括号合并同类项整式加减本章知识网络： 用字母表示数代数式整式单项式多项式列代数式代数式的值第一课时内容 用字母表示数的意义用字母表示数是基本数学思想之一，它使有些数量关系看起来更加简明，也更具有普遍意义。用字母表示：（ 1 ）乘法分配律()a bcabac（ 2 ）最小的数为 n 的五个连续的整数(4) (3) (2) (1)nnnnn、、、、n、(1)n  、(2)n 、(3)n  、 (4)n 、（ 3 ）最大的数为 n 的五个连续的整数（ 4 ）中间的数为 n 的五个连续的整数(2) (1)nn、、n、(n+1)、(n+2) 224ab2（）cm用字母表示图中阴影部分的面积：baab单位： cm 研究下列等式：21 3 1 42 ＋＝ ＝ ，22 4 1 9 3 ＋＝ ＝ ，23 5 1 164 ＋＝ ＝ ，24 6 1 25 5 ＋＝ ＝ ，则第 n 个等式用字母 n 可表示为2(2) 1(1)n nn ...用你观察到的规律写出第 100 个等式2100 102 1 101  用代数式表示下列问题的结果 :（ 2 ）比 a 、 b 两数和的 2 倍大 6 的数是（ 1 ）宽为 a 、长为 b 的长方形的面积是 （ 3 ）十位上的数字是 m ，个位上的数字比十位上的数字 大 4 的两位数是（ 4 ）某校七年级（ 1 ）班有 m 名女生，男生比女生的 一半多 5 人，则全班共有ab2(a+b)+610m+(m+4)(5)2mm 人 （ 5 ） a 与 b 、 c 两数之和的差（ 6 ） a 、 b 两数之差与 c 的和（ 7 ） a 、 b 两数的差的平方（ 8 ） a 、 b 两数的平方的差()abc()abc2()ab22ab 说出下面代数式的实际意义：4a+3b 代数式的值：求代数式24bac的值：（ 1 ）当 b=0,a=2,c= 16时；（ 2 ）当 b=-3 ， a=-5 ， c=2 时。解：（ 1 ）当 b=0,a=2,c=16时24bac=2104 2 ()6  = 4349 如图所示的计算程序，若开始输入的 x 的值为 5 ，则最后输出的结果是930是输出结果输入 x>200计算 的值(1)x x 否 用整体代入法求代数式的值已知 a+2b=3 ，求代数式 36ab的值。解： 当 a+2b=3 时363(2 )3 39abab 1 、 已知 a+2b-1=3 ，求代数式361ab的值。2 、解： 因为 a+2b-1=33613(2 ) 13 4 111abab  所以 a+2b=4 整式：单项式和多项式统称...