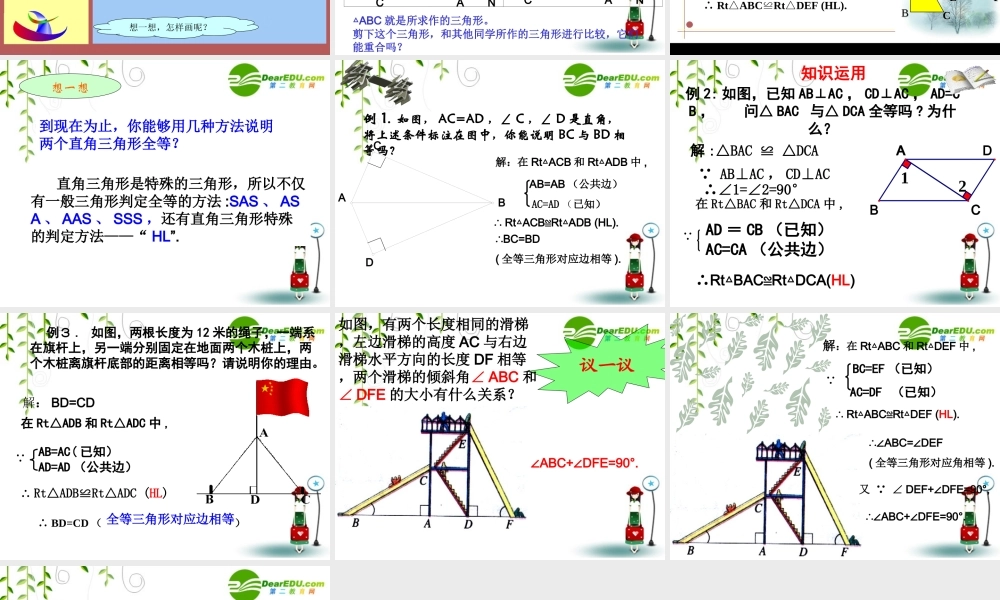
回回顾顾与与思思考考3 、如图, AB BE 于 C , DE BE, 垂足为 E ,⊥ ⊥ 2 、如图, Rt△ABC 中,直角边 、 ,斜边 。ABCBCACAB( 1 )若 A= D , AB=DE ,则 ABC 与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ ABCDEF全等ASA1 、全等三角形的对应边 ,对应角 。相等相等ABCDEF( 2 )若 A= D , BC=EF ,则 ABC 与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ AAS全等( 3 )若 AB=DE , BC=EF ,则 ABC 与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SAS( 4 )若 AB=DE , BC=EF , AC=DF则 ABC 与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SSS如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量 .( 1 )你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角 . (AAS)方法二:测量没遮住的一条直角边和一个对应的锐角 . (ASA) 或 (AAS)⑵ 如果他只带了一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的” . 你相信他的结论吗?下面让我们一起来验证这个结论。已知线段 a 、 c(ac)﹤和一个直角α ,利用尺规作一个 RtABC,△使∠ C= ∠ α , CB=a , AB=c.a(cα想一想,怎样画呢?按照下面的步骤做一做:⑴ 作∠ MCN=∠α=90°;CMN⑵ 在射线 CM 上截取线段 CB=a;CMNB⑶ 以 B 为圆心 ,C 为半径画弧,交射线 CN 于点 A;CMNBA⑷ 连接 AB.CMNBA△ABC 就是所求作的三角形。剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?直角三角形全等的条件斜边和一条直角边对应相等的两个直角三角形全等 . 简写成“斜边、直角边”或“ HL”.AABBCCDDEEFF AC=DF ( 已知) AB=DE (已知 )符号语言:在 RtABC△和 RtDEF△中 , ∴ RtABCRtDEF (HL).△≌△想一想到现在为止,你能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 :SAS 、 ASA 、 AAS 、 SSS ,还有直角三角形特殊的判定方法——“ HL”.例 1. 如图, AC=AD ,∠ C ,∠ D 是直角,将上述条件标注在图中,你能说明 B...