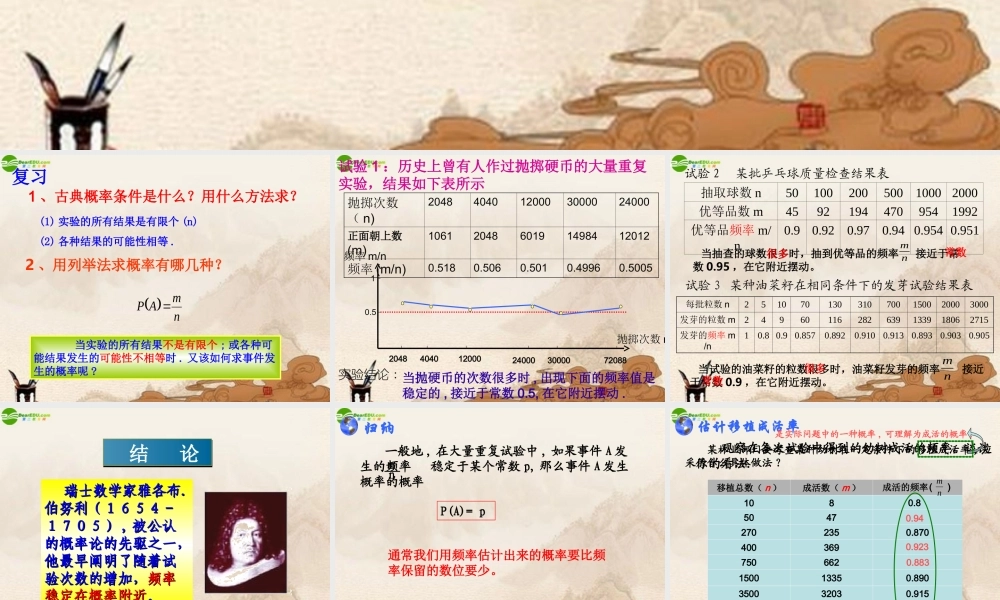
§25.3 利用频率估计概率 2 、用列举法求概率有哪几种? nmAP(1) 实验的所有结果是有限个 (n)(2) 各种结果的可能性相等 . 当实验的所有结果不是有限个 ; 或各种可能结果发生的可能性不相等时 . 又该如何求事件发生的概率呢 ?复习1 、古典概率条件是什么?用什么方法求?抛掷次数( n)20484040120003000024000正面朝上数(m)1061204860191498412012频率 (m/n)0.5180.5060.5010.49960.5005试验 1 :历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示抛掷次数 n频率 m/n0.512048404012000240003000072088实验结论 : 当抛硬币的次数很多时 , 出现下面的频率值是稳定的 , 接近于常数 0.5, 在它附近摆动 .试验 2 某批乒乓球质量检查结果表抽取球数 n5010020050010002000优等品数 m45921944709541992优等品频率 m/n0.90.920.970.94 0.954 0.951试验 3 某种油菜籽在相同条件下的发芽试验结果表每批粒数 n251070130310700150020003000发芽的粒数 m24960116282639133918062715发芽的频率 m/n10.8 0.9 0.8570.8920.9100.9130.8930.9030.905 当抽查的球数很多时,抽到优等品的频率 接近于常数 0.95 ,在它附近摆动。nm 很多常数 当试验的油菜籽的粒数很多时,油菜籽发芽的频率 接近于常数 0.9 ,在它附近摆动。nm很多 常数 结 论 结 论 瑞士数学家雅各布.瑞士数学家雅各布.伯努利(1654-伯努利(1654-1705)1705) ,, 被公认被公认的概率论的先驱之一,的概率论的先驱之一,他最早阐明了随着试他最早阐明了随着试验次数的增加,验次数的增加,频率频率稳定在概率附近稳定在概率附近。。归纳 一般地 , 在大量重复试验中 , 如果事件 A 发生的频率 稳定于某个常数 p, 那么事件 A 发生概率的概率P(A)= p mn通常我们用频率估计出来的概率要比频率保留的数位要少。 某林业部门要考查某种幼树在一定条件下的移植成活率 , 应采用什么具体做法 ? 观察在各次试验中得到的幼树成活的频率,谈谈你的看法.估计移植成活率移植总数( n )成活数( m )108成活的频率0.8( )nm50472702350.870400369750662150013350.890350032030.915700063359000807314000126280.9020.940.9230.8830.9050.897是实际问题中的一种概率 , 可理解为成活的概率 .估计移植成活率 由下表可以发现,幼树移植成活的频率在____左右摆动,并且随着移植棵数越来越大,这种...