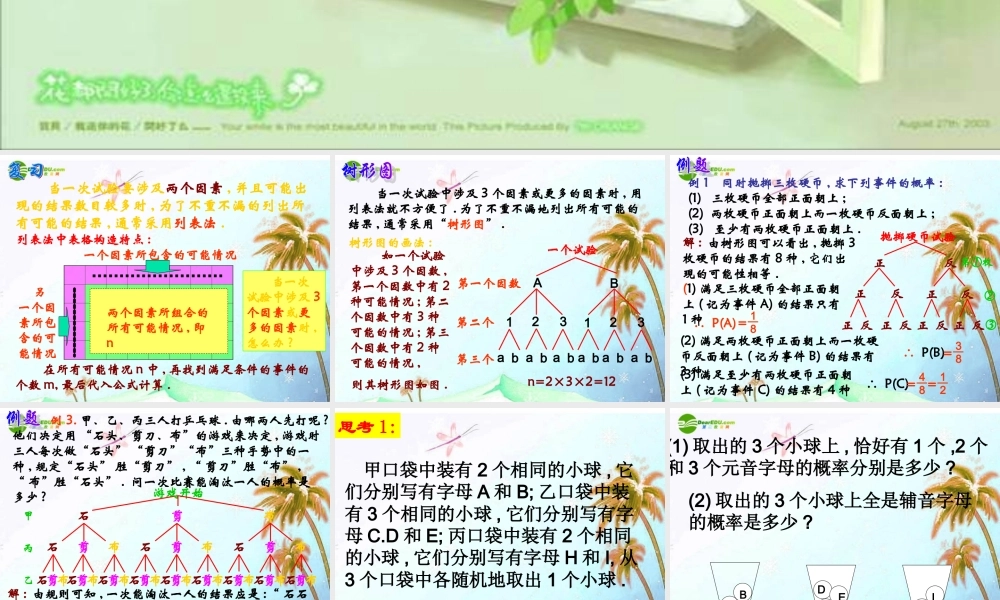
当一次试验要涉及两个因素 , 并且可能出现的结果数目较多时 , 为了不重不漏的列出所有可能的结果 , 通常采用列表法 .一个因素所包含的可能情况 另一个因素所包含的可能情况两个因素所组合的所有可能情况 , 即n 在所有可能情况 n 中 , 再找到满足条件的事件的个数 m, 最后代入公式计算 .列表法中表格构造特点 : 当一次试验中涉及 3个因素或更多的因素时 ,怎么办 ? 当一次试验中涉及 3 个因素或更多的因素时 , 用列表法就不方便了 . 为了不重不漏地列出所有可能的结果 , 通常采用“树形图” .树形图的画法 :一个试验第一个因数第二个第三个 如一个试验中涉及 3 个因数 ,第一个因数中有 2种可能情况 ; 第二个因数中有 3 种可能的情况 ; 第三个因数中有 2 种可能的情况 ,AB123123a b a b a b a b a b a b则其树形图如图 .n=2×3×2=12例 1 同时抛掷三枚硬币 , 求下列事件的概率 :(1) 三枚硬币全部正面朝上 ;(2) 两枚硬币正面朝上而一枚硬币反面朝上 ;(3) 至少有两枚硬币正面朝上 .正 反 正 反 正 反 正 反正反正反正反抛掷硬币试验解 : 由树形图可以看出 , 抛掷 3枚硬币的结果有 8 种 , 它们出现的可能性相等 .∴ P(A)(1) 满足三枚硬币全部正面朝上 ( 记为事件 A) 的结果只有1 种18=∴ P(B)38=(2) 满足两枚硬币正面朝上而一枚硬币反面朝上 ( 记为事件 B) 的结果有3 种(3) 满足至少有两枚硬币正面朝上 ( 记为事件 C) 的结果有 4 种∴ P(C)48=12=第①枚②③ 例 3. 甲、乙、丙三人打乒乓球 . 由哪两人先打呢 ?他们决定用 “石头、剪刀、布”的游戏来决定 , 游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种 , 规定“石头” 胜“剪刀” , “ 剪刀”胜“布” , “ 布”胜“石头” . 问一次比赛能淘汰一人的概率是多少 ?石剪布石游戏开始甲乙丙石石剪布石剪布石剪布石剪布石剪布石剪布石剪布石剪布剪布石剪布石剪布剪布解 : 由树形图可以看出 , 游戏的结果有 27 种 , 它们出现的可能性相等 . 由规则可知 , 一次能淘汰一人的结果应是 :“ 石石剪” “剪剪布” “布布石”三类 . 而满足条件 ( 记为事件A) 的结果有 9 种 ∴ P(A)=13=927 甲口袋中装有 2 个相同的小球 , 它们分别写有字母 A 和 B; 乙口袋中装有 3 个相同的小球 , 它们分别写有字母 C.D 和 E; 丙口袋...