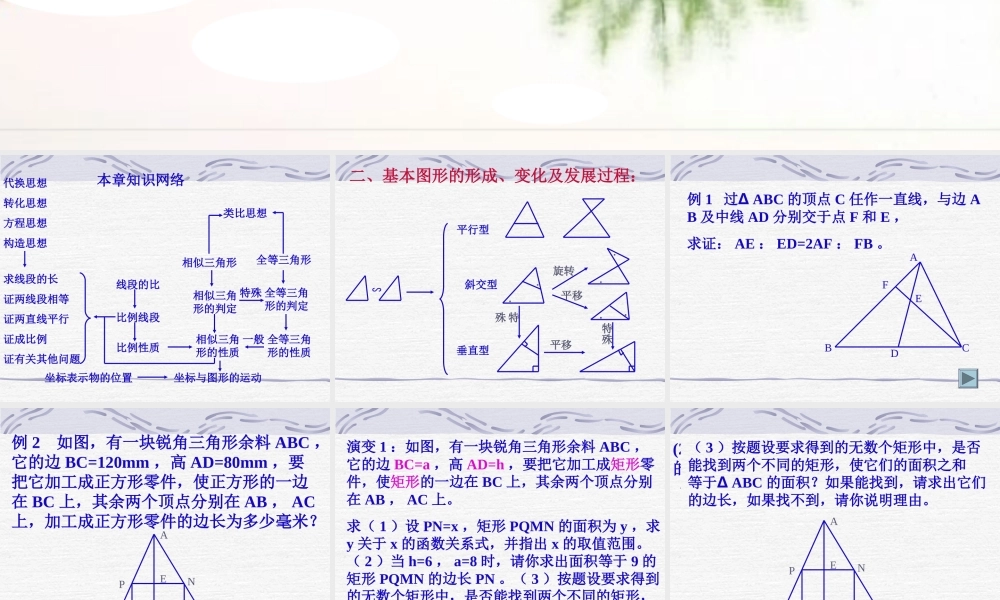
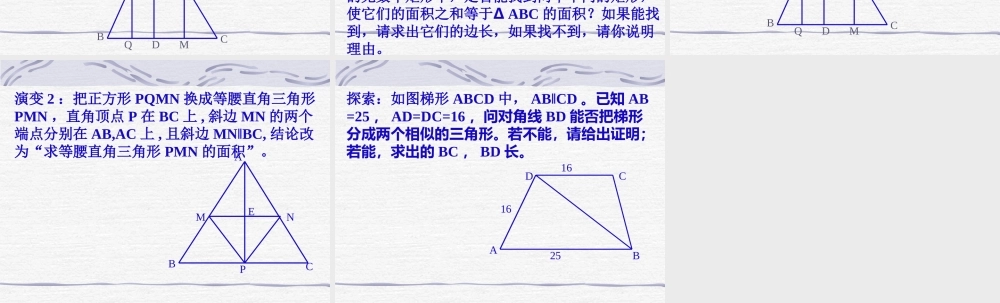
相似三角形 代换思想转化思想方程思想构造思想求线段的长证两线段相等证两直线平行证成比例证有关其他问题比例线段线段的比比例性质相似三角形的性质相似三角形的判定相似三角形全等三角形的性质全等三角形的判定全等三角形类比思想特殊一般坐标与图形的运动坐标表示物的位置本章知识网络 二、基本图形的形成、变化及发展过程:∽ 平行型 斜交型. . . . . . 旋转平移垂直型特殊特殊平移 例 1 过∆ ABC 的顶点 C 任作一直线,与边 AB 及中线 AD 分别交于点 F 和 E ,求证: AE : ED=2AF : FB 。CABFDE 例 2 如图,有一块锐角三角形余料 ABC ,它的边 BC=120mm ,高 AD=80mm ,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB , AC上,加工成正方形零件的边长为多少毫米?ABCDEPQMN 演变 1 :如图,有一块锐角三角形余料 ABC ,它的边 BC=a ,高 AD=h ,要把它加工成矩形零件,使矩形的一边在 BC 上,其余两个顶点分别在 AB , AC 上。求( 1 )设 PN=x ,矩形 PQMN 的面积为 y ,求y 关于 x 的函数关系式,并指出 x 的取值范围。( 2 )当 h=6 , a=8 时,请你求出面积等于 9 的矩形 PQMN 的边长 PN 。( 3 )按题设要求得到的无数个矩形中,是否能找到两个不同的矩形,使它们的面积之和等于∆ ABC 的面积?如果能找到,请求出它们的边长,如果找不到,请你说明理由。 求( 1 )设 PN=x ,矩形 PQMN 的面积为 y ,求 y 关于 x 的函数关系式,并指出 x 的取值范围。ABCDEPQMN(2) 当 h=6 , a=8 时,请你求出面积等于 9的矩形 PQMN 的边长 PN 。( 3 )按题设要求得到的无数个矩形中,是否能找到两个不同的矩形,使它们的面积之和等于∆ ABC 的面积?如果能找到,请求出它们的边长,如果找不到,请你说明理由。 演变 2 :把正方形 PQMN 换成等腰直角三角形PMN ,直角顶点 P 在 BC 上 , 斜边 MN 的两个端点分别在 AB,AC 上 , 且斜边 MN‖BC, 结论改为“求等腰直角三角形 PMN 的面积”。CABPMNE 探索:如图梯形 ABCD 中, AB‖CD 。已知 AB=25 , AD=DC=16 ,问对角线 BD 能否把梯形分成两个相似的三角形。若不能,请给出证明;若能,求出的 BC , BD 长。BDCA161625