广东省高三数学 第2章第2节函数的奇偶性与周期性复习课件 理 课件VIP免费

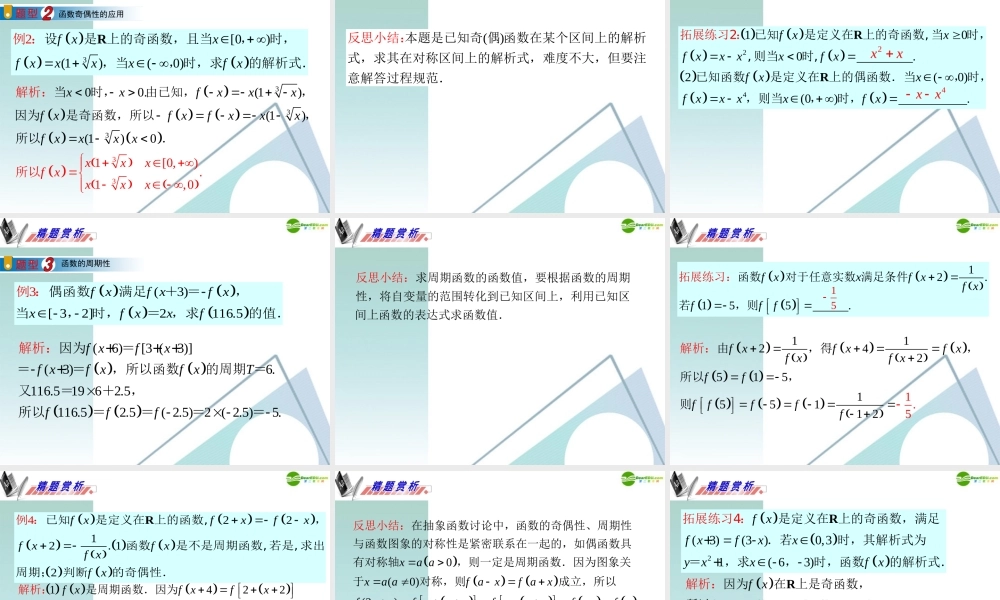
  31.sin1()2 A 3 B 0 C1 D2f xxxxf afa函数，若，则的值为....RB      33332sin12sin1sin1s1in11 10.11120B 2.f aaaaafaaaaah xf xfahah af a       因为，即，所以，所以易知为奇函数，方法 ：方法 ：所析：，故选以解          2.20,2 A012 B102C120 D210yf xyf xffffffffffff 已知函数是偶函数，在上是单调递减函数，则....A    20,22,00,21 A.1f xf xyf xf xff由于在上单调递减，所以在上单调递减．因为是偶函数，所以在上单调递解析：故又，应选增．     3.21,316 A 1 B3 C1 D. 3f xf xf xxf xxf 已知函数满足．当时，，则．．．D    2424622D .3f xf xf xf xf xf xfff由，得，所以的周期为 ，所以解，析：故选  24.3[1,2 ] 1A 0 B. C 1 D13f xaxbxabaaab 已知函数是定义域为的偶函数，则的值是．．． 23[1,2 ]10133.12f xaxbxabaabaaaab由函数是定义域为的偶函数，得，并且，即，所以的值是解析：B   25.1 .fxxxaa设函数为奇函数，则    2210001 000.f xxxafaa由函数为奇函数，得即，得，解析：0 判断函数的奇偶性          221111)lg101212(1)130214:.xxxxxxx xxx xf xf xxf xf x   判断下列函数的奇偶性．＝； ＝ －；＝；＝－例      11011.()lglg()lg20111111111111.xxxxxxf xfxf xxfxxxxxx －由，得-故的定义域关于原点对称．又-＝＝＝-＝-，由，得-故的定义域不关于原点对称，解析：故原函数是奇函数．故原函数是非奇非偶函数．         22223(0)(0)000()00041112121122112()()22xx...