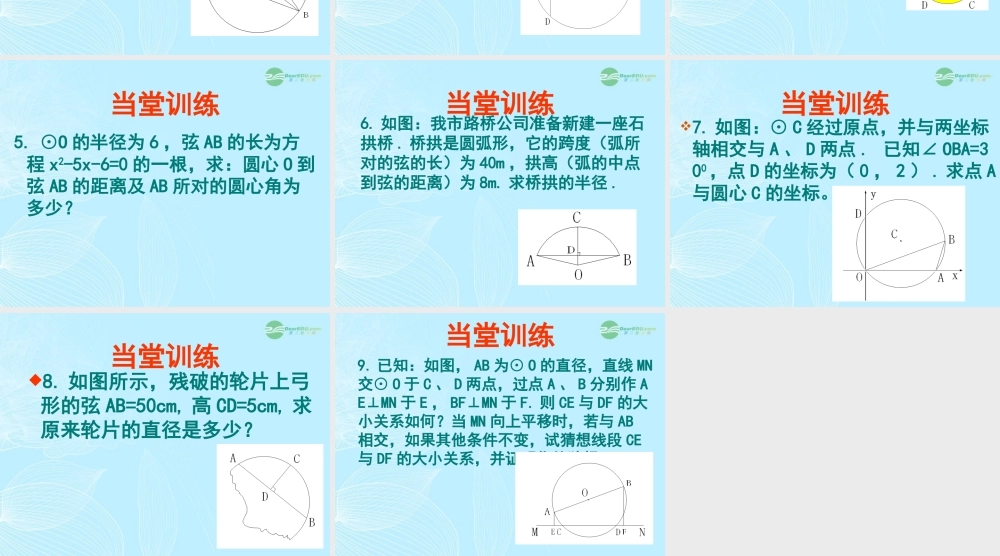
28.1 圆的认识——圆周角( 2 )学习目标灵活运用圆周角的定义、性质解决有关圆的问题。自学指导认真阅读并思考下列问题:1. 什么叫圆周角?2. 圆周角有什么性质?当堂训练1. 下列结论中,正确的有( )①. 顶点在圆周的角叫圆周角。②. 圆周角的度数等于圆心角度数的一半。③.900的圆周角所对的弦是直径。④. 圆周角相等,则它们所对的弧也相等。 A.1 个 B.2 个 C.3 个 D.4 个A当堂训练2. 如图, D 是 的中点,与 相等的角有( )A 、 7 个 B 、 3 个C 、 2 个 D 、 1 个ABDB当堂训练 3. 如图, AB 是⊙ O 的直径,弦 CD⊥AB 于P. 已知 CD=8cm ,∠ B=300. 求⊙ O 的半径 .当堂训练 4. 如图,是中国共产主义青年团团旗上的图案,点 A 、 B 、 C 、 D 、 E 五等分圆,则∠ A+∠B+∠C+∠D+∠E 的度数是( )。 A 、 1800 B 、 1500 C 、 1350 D 、 1200当堂训练5. ⊙O 的半径为 6 ,弦 AB 的长为方程 x2-5x-6=0 的一根,求:圆心 O 到弦 AB 的距离及 AB 所对的圆心角为多少?当堂训练6. 如图:我市路桥公司准备新建一座石拱桥 . 桥拱是圆弧形,它的跨度(弧所对的弦的长)为 40m ,拱高(弧的中点到弦的距离)为 8m. 求桥拱的半径 .当堂训练7. 如图:⊙ C 经过原点,并与两坐标轴相交与 A 、 D 两点 . 已知∠ OBA=300,点 D 的坐标为( 0 , 2 ) . 求点 A与圆心 C 的坐标。当堂训练8. 如图所示,残破的轮片上弓形的弦 AB=50cm, 高 CD=5cm, 求原来轮片的直径是多少?当堂训练9. 已知:如图, AB 为⊙ O 的直径,直线 MN交⊙ O 于 C 、 D 两点,过点 A 、 B 分别作 AE⊥MN 于 E , BF⊥MN 于 F. 则 CE 与 DF 的大小关系如何?当 MN 向上平移时,若与 AB相交,如果其他条件不变,试猜想线段 CE与 DF 的大小关系,并证明你的猜想。