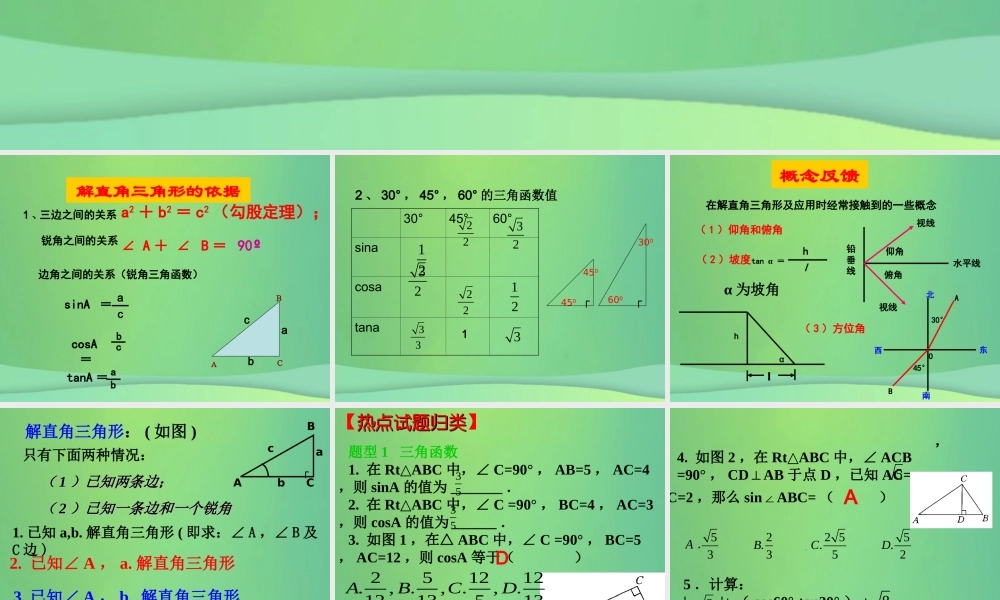
三边之间的关系 a2 + b2 = c2 (勾股定理);锐角之间的关系 ∠ A + ∠ B = 90º边角之间的关系(锐角三角函数)tanA = absinA = ac1 、cosA=bcACBabc解直角三角形的依据2 、 30° , 45° , 60° 的三角函数值30°45°60°sinacosatana2232333123222121┌┌450450300600在解直角三角形及应用时经常接触到的一些概念lhα( 2 )坡度tan α =hl概念反馈( 1 )仰角和俯角视线铅垂线水平线视线仰角俯角( 3 )方位角30°45°BOA东西北南α 为坡角解直角三角形: ( 如图 )1. 已知 a,b. 解直角三角形 ( 即求:∠ A ,∠ B 及C 边 )2. 已知∠ A , a. 解直角三角形 3. 已知∠ A , b. 解直角三角形4. 已知∠ A , c. 解直角三角形bABCa┌c只有下面两种情况: (( 11 )已知两条边;)已知两条边; (( 22 )已知一条边和一个锐角)已知一条边和一个锐角【热点试题归类热点试题归类】题型 1 三角函数1. 在 Rt ABC△中,∠ C=90° , AB=5 , AC=4,则 sinA 的值为 _______ .2. 在 Rt ABC△中,∠ C =90° , BC=4 , AC=3,则 cosA 的值为 ______ .3. 如图 1 ,在△ ABC 中,∠ C =90° , BC=5, AC=12 ,则 cosA 等于( ) 1312.,512.,135.,122.DCBA35 35D4. 如图 2 ,在 Rt ABC△中,∠ ACB =90° , CDAB⊥于点 D ,已知 AC=5BC=2 ,那么 sinABC=∠( ), A .522 55...3352BCD 5 .计算:|-28|+ ( cos60°-tan30° ) +.A 123题型 2 解直角三角形1. 如图 4 ,在矩形 ABCD 中 DEAC⊥于 E , 设∠ ADE=a , 且cosα=35AB=4 ,则 AD 的长为( ),162016..335CDA . 3 B .B题型 3 解斜三角形1. 如图 6 所示,已知:在△ ABC 中,∠ A=60° ,∠ B=45° , AB=8 , 求△ ABC 的面积(结果可保留根号).2. 如图,海上有一灯塔 P ,在它周围 3 海里处有暗礁, 一艘客轮以 9海里 / 时的速度由西向东航行,行至A 点处测得 P 在它的北偏东 60° 的方向,继续行驶 20 分钟后,到达 B 处又测得灯塔 P 在它的北偏东 45° 方向,问客轮不改变方向继续前进有无触礁的危险?解:过C作CD⊥AB于D, 设CD=x.在Rt△ACD中,cot60°=ADCD3 在 RtBCD△中, BD=CD=x . ∴33x+x=8 . 解得 x=4 ( 3- ).33=16 ( 3-) ...