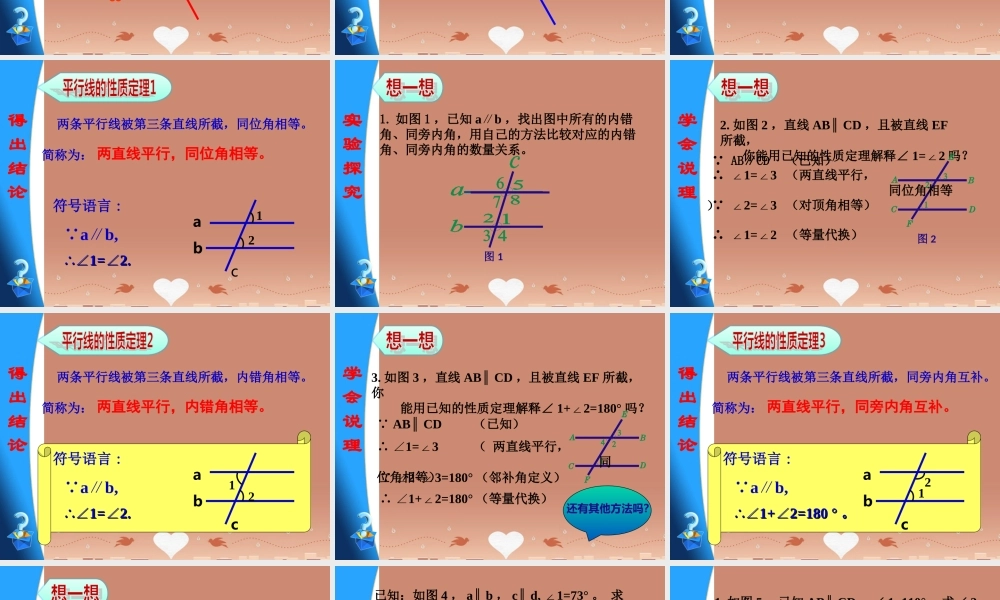
第七章 相交线与平行线第第 55 节 平行线的性质节 平行线的性质 建筑数学 世界著名的意大利比萨斜塔,建于公元 1173 年,为8层圆柱形建筑,全部用白色大理石砌成,塔高 54.5 米。12逆向思考1. 你学会了哪些判定两直线平行的方法?同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。2. 现在我们逆向思考,把这些命题中的条件和结论互换,你能得出哪些命题?两直线平行, 同位角相等;两直线平行, 内错角相等;两直线平行,同旁内角互补。观察猜想猜一猜:当 ab∥ 时,∠∠ 11 和∠和∠ 22 的的大小有何关系?大小有何关系?b12ac 心动 不如行动动手操作65°65°cab12b2ac1动手操作思考发现 通过刚才的观察猜想、动手操作、小组合作,你得出了什么结论?得出结论 两条平行线被第三条直线所截,同位角相等。b12ac简称为:符号语言 :∴∴∠∠1=2.∠1=2.∠ ab,∥两直线平行,同位角相等。实验探究1. 如图 1 ,已知 ab∥ ,找出图中所有的内错角、同旁内角,用自己的方法比较对应的内错角、同旁内角的数量关系。图 1学会说理2. 如图 2 ,直线 AB∥ CD ,且被直线 EF所截, 你能用已知的性质定理解释∠ 1=∠2 吗?图 2 AB∥CD (已知)∴ ∠1=∠3 (两直线平行, 同位角相等) ∠2=∠3 (对顶角相等) ∴ ∠1=∠2 (等量代换)得出结论 两条平行线被第三条直线所截,内错角相等。简称为:b2ac1符号语言 :∴∴∠∠1=2.∠1=2.∠ ab,∥两直线平行,内错角相等。如图 3 ,学会说理3. 如图 3 ,直线 AB∥ CD ,且被直线 EF 所截,你 能用已知的性质定理解释∠ 1+∠2=180° 吗?图 3 AB∥ CD (已知)还有其他方法吗? ∴ ∠1=∠3 ( 两直线平行, 同位角相等) ∠2+∠3=180° (邻补角定义) ∴ ∠1+∠2=180° (等量代换)得出结论 两条平行线被第三条直线所截,同旁内角互补。简称为:2b1ac符号语言 :∴∴∠∠11++2∠2∠ =180 °=180 ° 。。 ab,∥两直线平行,同旁内角互补。活动二:对比分析平行线的判定和性质有什么联系和区别? 条件结论判定同位角相等两直线平行内错角相等同旁内角互补性质两直线平行同位角相等内错角相等同旁内角互补有理有据已知:如图 4 , a∥ b , c∥ d, ∠1=73° 。 求 ∠2 和∠ 3 的度数。图 4解: a∥ b (已知), ∴ ∠1=∠2 (两直线平行, 内错角相等)。...