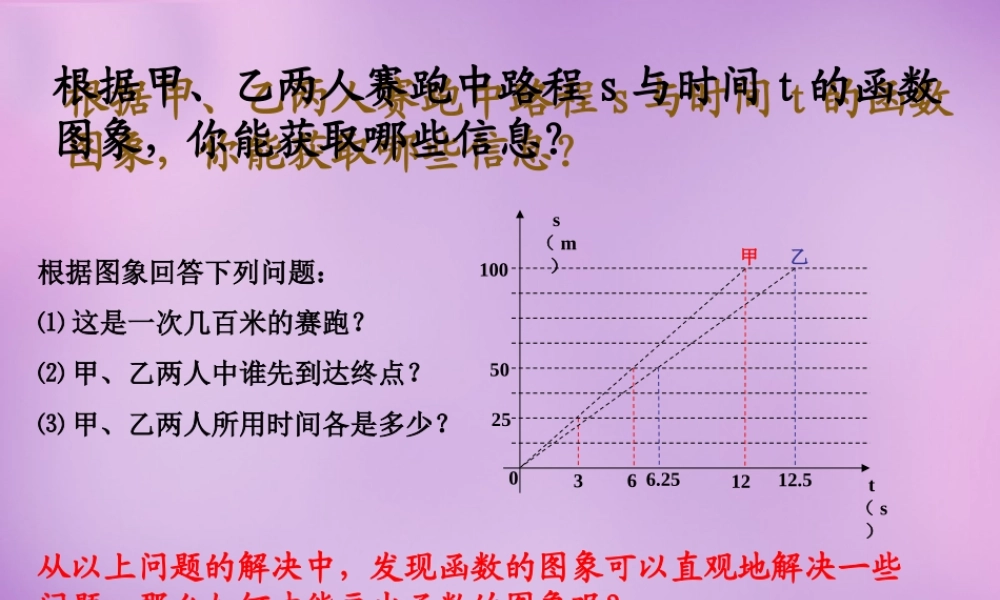
根据甲、乙两人赛跑中路程 s 与时间 t 的函数图象,你能获取哪些信息?根据甲、乙两人赛跑中路程 s 与时间 t 的函数图象,你能获取哪些信息?根据图象回答下列问题:⑴ 这是一次几百米的赛跑?⑵ 甲、乙两人中谁先到达终点?⑶ 甲、乙两人所用时间各是多少?从以上问题的解决中,发现函数的图象可以直观地解决一些问题。那么如何才能画出函数的图象呢?0501001212.56 6.25t( s)s( m)甲乙253参照图象甲为例,当 t=3 时, s=25 ,这样把自变量 t 作为点的横坐标,把函数 s 作为点的纵坐标就得到点( 3 , 25 )0501001212.56 6.25t( s)s( m)甲乙253当 t=6 时, s=50 ,就得到点( 6 , 50 )……,所有这些点就组成了这个函数的图象。 像这样,把一个函数的自变量 x 与对应的函数 y 的值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象。函数的图象是我们研究和处理有关函数问题的重要工具。合作学习作一次函数 y=2x 的图象:x…-2-1012…y =2x…-4-20…(x ,y)……注、分别以表中的 x 值作点的 横坐标 ,对应的 y 值作点的 纵坐标 ,得到一组点,写出这组点的坐标。2 、画一个直角坐标系,并在直角坐标系中画出这组点。24( -1 , -2 )( 0 ,0 )( 1 ,2 )( 2 ,4 )( -2 , -4 )1 、选择 5 对自变量与函数的对应值,完成下表-5 -4 -3 -2 -1 0 1 2 3 4 5 x 5 4 3 2 1 -1 -2 -3 -4 -5yy=2x以上画函数图象的方法叫做描点法。(1) 列表;( 2 )描点;( 3 )连线;-5 -4 -3 -2 -1 0 1 2 3 4 5 x 5 4 3 2 1 -1 -2 -3 -4 -5yy=2x1 、观察上面图像,有特殊点吗?经过哪几个象限?2 、点( 3 , 6 )在图像上吗?3 、点( 10,20) 呢 ?……坐标满足一次函数 y=2x 的各点都在直线上。x….-2-1012….y=2x+1….….-3-1135作一次函数 y=2X+1 的图象(-2,-3) (-1,-1) (0,1) (1,3) (2,5)以自变量 x 与对应的函数 y 的值作为点的横坐标和纵坐标,……在直角坐标系中描出对应点,所有这些点组成的图形叫做这个函数的图象合作学习8642-2-4-6-8-10-5510yXOY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612 3 45678-7-8Y=2X8642-2-4-6-8-10-5510yXOY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345...