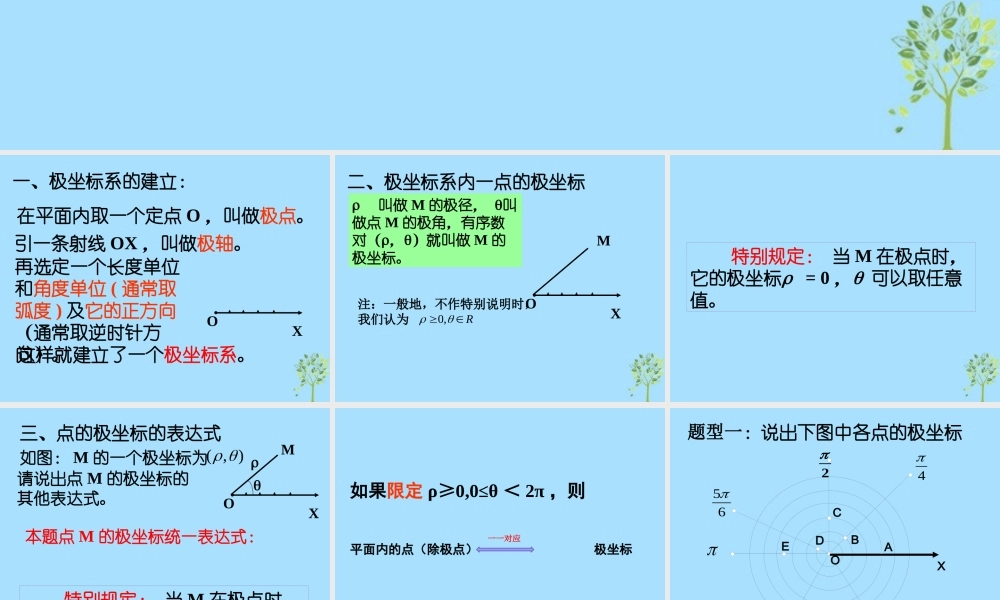
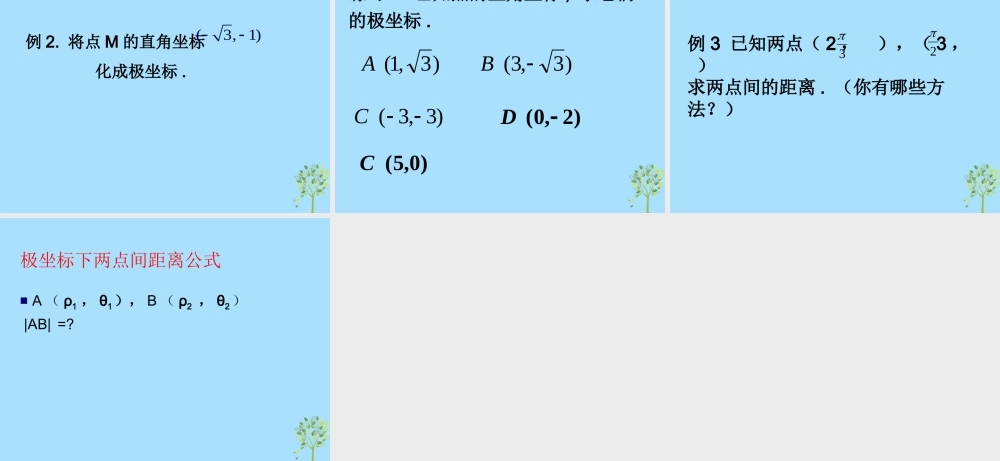
极坐标系一、极坐标系的建立:在平面内取一个定点 O ,叫做极点。引一条射线 OX ,叫做极轴。再选定一个长度单位和角度单位 ( 通常取弧度 ) 及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。XO二、极坐标系内一点的极坐标XOM 叫做 M 的极径, 叫做点 M 的极角,有序数对(,)就叫做 M 的极坐标。注:一般地,不作特别说明时,我们认为R ,0 特别规定: 当 M 在极点时,它的极坐标 = 0 , 可以取任意值。三、点的极坐标的表达式XOM如图: M 的一个极坐标为请说出点 M 的极坐标的其他表达式。本题点 M 的极坐标统一表达式:),( 特别规定: 当 M 在极点时,它的极坐标 = 0 , 可以取任意值。如果限定 ρ≥0,0≤θ < 2π ,则平面内的点(除极点) 极坐标一一对应题型一:说出下图中各点的极坐标ABCDEFGOX46535342题型二:在极坐标系里描出下列各点)26,4()46,4()26,4(6,4),4()2,3()2,6()0,3()(ABCDEFGOX46535342四、极坐标和直角坐标的互化平面内的一个点的直角坐标是 (1, )3这个点如何用极坐标表示 ?思考:极坐标与直角坐标的互化关系式 :设点 M 的直角坐标是 (x, y) 极坐标是 (ρ,θ)x=ρcosθ, y=ρsinθ )0(tan,222xxyyx注:互化公式的三个前提条件:1. 极点与直角坐标系的原点重合 ;2. 极轴与直角坐标系的 x 轴的正半 轴重合 ;3. 两种坐标系的单位长度相同 .例 1. 将点 M 的极坐标 化成直角坐标 .2(5,)3练习:已知下列点的极坐标,求它们的直角坐标。)6,3(A)2,2(B)2,1(C)4,23(D例 2. 将点 M 的直角坐标 化成极坐标 .(3, 1)练习 : 已知点的直角坐标 , 求它们的极坐标 .)3,3( B)3,1(A)0,5(C)2,0( D)3,3(C例 3 已知两点( 2 , ),( 3 , )求两点间的距离 . (你有哪些方法?)32极坐标下两点间距离公式 A ( ρ1 , θ1), B ( ρ2 , θ2) |AB| =?