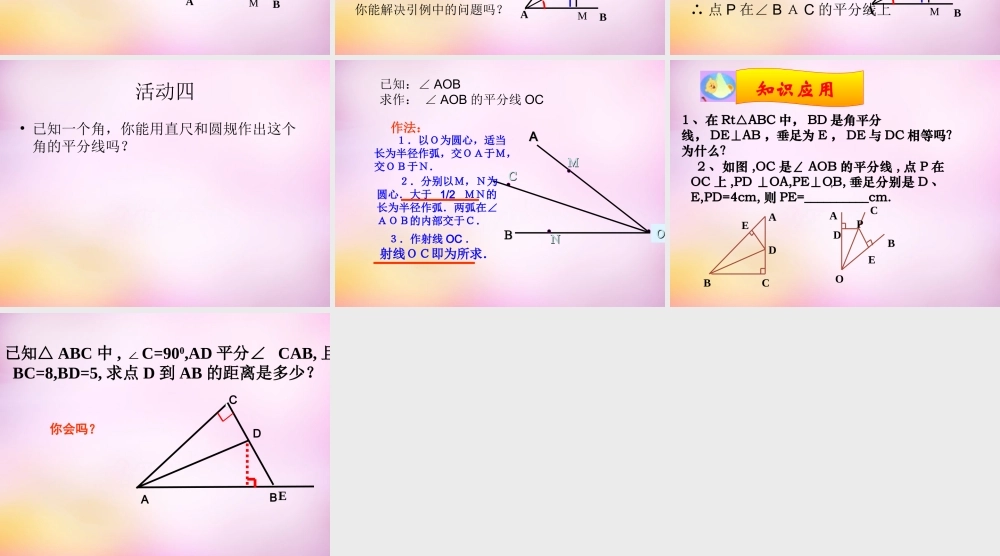
教学目标•1. 能够通过折纸、画图等操作,体会角的对称性,从而认识角平分线的性质;•2. 能够利用尺规作图,作出角的平分线;运用作图和实验的方法,探索线段的垂直平分线的性质定理和逆定理;活动一• 1.1. 不利用工具,请你将一张用纸片做的角不利用工具,请你将一张用纸片做的角∠ BAC 分成两个相等的角。你有什么办法?分成两个相等的角。你有什么办法?• 2. 2. 再再把纸片展开后铺平,记折痕为 AD 。• 3. 你发现∠ BAC 是轴对称图形吗?• 4. 如果是,它的对称轴是那一条直线?• 5. 归纳 : 角是轴对称图形,角平分线 所在的直线是它的对称轴。BAC活动二• 1 .在角平分线上任意取点 P ,过点 P 作 PMAB⊥, PNAC,⊥垂足分别是 M , N , 动手量一量,折一折• 2. 用圆规比较 PM 与 PN 的大小你发现什么? 请你给你同桌说明你的理由?• 3. 如何转化为几何符号语言 (提醒同学们注意条件和结论)• 4. 你得到什么结论NPMCABD结论:角平分线上的点,到这个角的两边的距离相等。强调:( 1 )是点在角平分线上;( 2 )是这一点到角两边的距离相等。 这里“距离”指的是角平分线上的点到角两边的垂线段的长度。用数学语言表示∵ AD是∠ B A C 的平分线P M⊥AB, P N⊥AC∴ P M =P N 你能解决引例中的问题吗?NPMCABD活动三1. 请同学们阅读课本 52 页第( 3 ),画一画,折一折,猜一猜2.你知道这一问题中的已知和结论吗?3. 你能说出这一结论文字语言和数学语言吗?• 角的内部到角的两边距离相等的点在这个角的平分线上。 如图 用数学语言表示∵P M⊥AB, P N⊥ACP M =P N∴ 点 P 在∠ B A C 的平分线上NPMCABD活动四• 已知一个角,你能用直尺和圆规作出这个角的平分线吗?AABBOOMMNNCC作法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线 OC .射线OC即为所求. 已知:∠ AOB求作: ∠ AOB 的平分线 OC ,1 、在 Rt△ABC 中, BD 是角平分线, DE⊥AB ,垂足为 E , DE 与 DC 相等吗?为什么? ABCDE 2 、如图 ,OC 是∠ AOB 的平分线 , 点 P 在OC 上 ,PD ⊥OA,PE⊥OB, 垂足分别是 D 、E,PD=4cm, 则 PE=__________cm.ADOBEPC知识应用3. 已知△ ABC 中 , C=90∠0,AD 平分∠ CAB, 且 BC=8,BD=5, 求点 D 到 AB 的距离是多少?EABCD你会吗?