八年级数学下册 3.1 同底数幂的乘法(第1课时)课件 (新版)浙教版 课件VIP免费

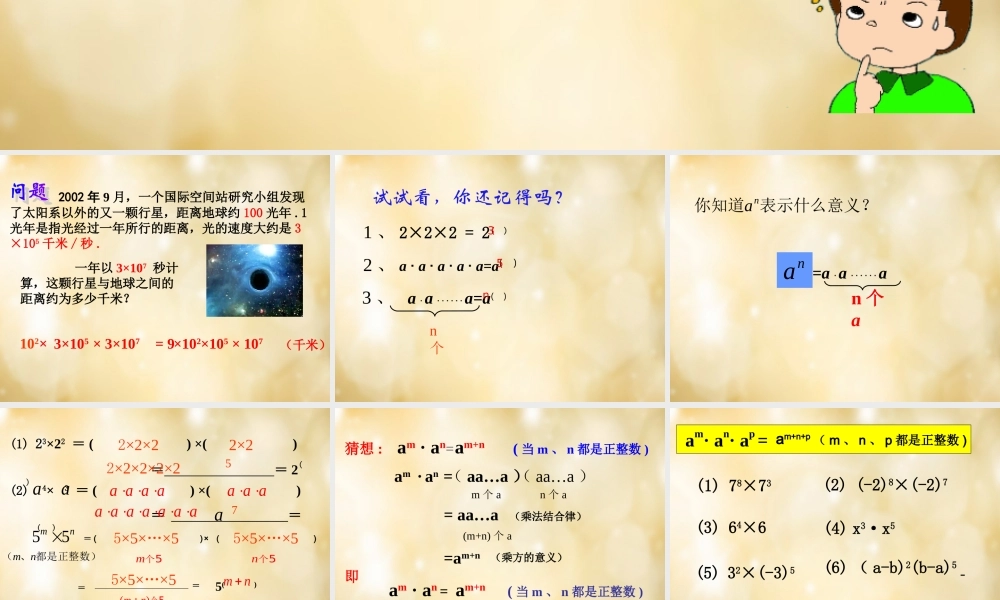
2002 年 9 月，一个国际空间站研究小组发现了太阳系以外的又一颗行星，距离地球约 100 光年 .1光年是指光经过一年所行的距离，光的速度大约是 3×105 千米 / 秒 . 一年以 3×107 秒计算，这颗行星与地球之间的距离约为多少千米？= 9×102×105 × 107 3×105 × 3×107102×（千米）试试看，你还记得吗？1 、 2×2×2 = 2( )2 、 a · a · a · a · a=a( ) 3 、 a · a · · · · · · a=a( ) n个35nna表示什么意义？你知道na=a · a · · · · · · an 个a(1) 23×22 ＝ ( ) ×( ) ＝ ＝ 2( )(2) 4× 3 ＝ ( ) ×( ) ＝ ＝ ( )aaa55mnmn（ 、 都是正整数）2×2×22×22×2×2×2×25a a a a  a a a a a a a a a a     75×5×…×55×5×…×5m个5n个55×5×…×5()mn个5mn5( )＝ ( ) ( )×＝＝猜想：am · an ＝ （ m 、 n 都是正整数）?am+n 猜想 : am · an= ( 当 m 、 n 都是正整数 ) am · an =m 个 an 个 a= aa…a=am+n(m+n) 个 a即am · an = am+n ( 当 m 、 n 都是正整数 )（ aa…a ）（ aa…a ）am+n（乘法结合律）（乘方的意义）例 1 、计算： (1) 78×73 (3) 64×6(2) (-2)8×(-2)7(5) 32×(-3)5 (6) （ a-b)2(b-a)5 (4) x3·x5am· an· ap = am+n+p （ m 、 n 、 p 都是正整数 ) （ 2 ） x5 × (-x)6（ 1 ） (-10)5×(-10)6(3) (a-2b)(2b-a)2练习一 ：计算(4) (-5)10 ×(-52) ×53 练习二下面的计算对不对？如果不对，怎样改正？（ 1 ） b5 · b5= b10 （ ） （ 2 ） b5 + b5 = b10 （ ）（ 3 ） a ·(- a)7 = a8 ( ) （ 4 ） m + m3 = m4 ( ) （ 5 ） 3a2·a3- a3·a2 = 0( ) √ × b5 + b5 = 2b5× × m + m3 = m + m3 √通过上面的练习你认为同底数幂的乘法法则的应用应注意什么 ?1. 同底数幂相乘时 , 指数是相加的2. 注意 am · an 与 am + an 的区别3. 不能疏忽指数为 1 的情况火眼金睛 a ·(- a7) = -a8 2002 年 9 月，一个国际空间站研究小组发现了太阳系以外的第 100 颗行星，距离地球约 100光年 .1 光年是指光经过一年所行的距离，光的速度大约是 3×105 千米 / 秒 ....