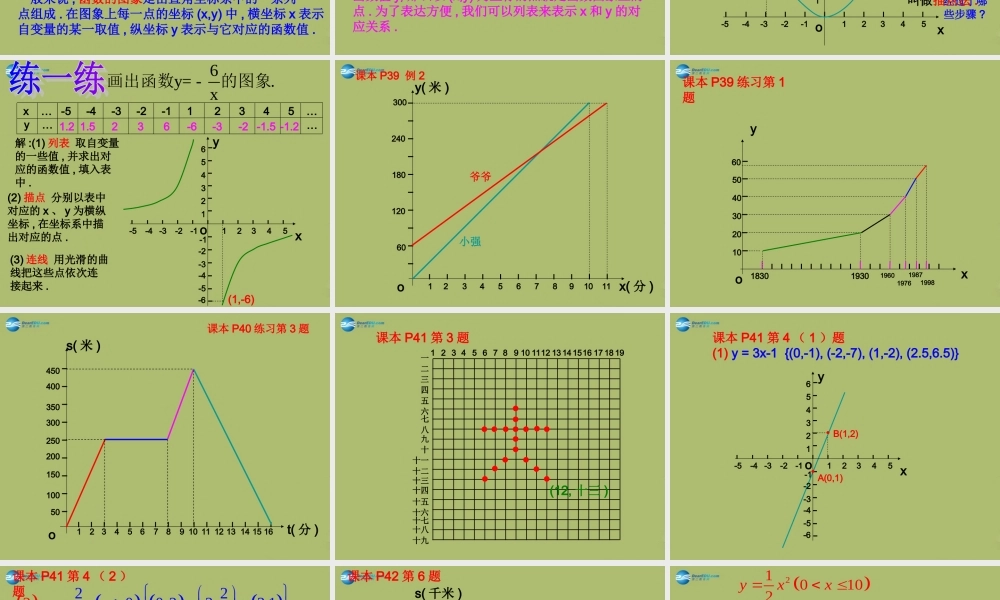
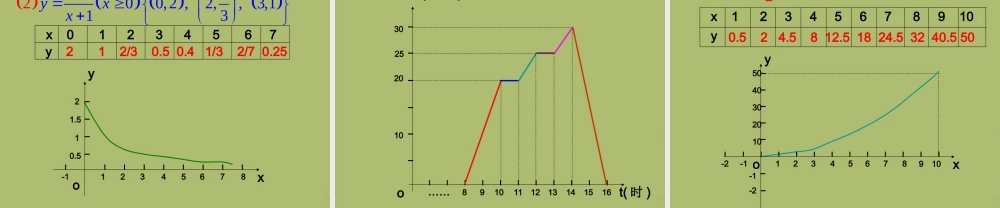
函数的图象第 17 章 函数及其图象17.2 函数的图象(第 2 课时) 2 、如果在某一变化过程中,有两个变量,如 x 和 y ,对于 x 的每一个值, y 都有唯一的值与之对应,我们就说 x 是自变量, y 是因变量,此时也称 y 是 x 的函数. 3 、函数关系的三种表示方法 :解析法、列表法、图象法 1 、在某一变化过程中 , 可以取不同数值的量 , 叫做变量 . 还有一种量,它的取值始终保持不变,称之为常量 .变量与函数1 、能够正确画出直角坐标系。2 、能在直角坐标系中,根据坐标作出点, 由点求出坐标。3 、掌握各象限上及 x 轴, y 轴上点的坐标的 特点: 第一象限( + , + ) 第二象限(- , + ) 第三象限(- , -)第四象限( + , -) x 轴上的点纵坐标为 0 ,表示为( x , 0 ) y 轴上的点横坐标为 0 ,表示为( 0 , y )平面直角坐标系4 、平行于横轴的直线上的点的纵坐标相同; 平行于纵轴的直线上的点的横坐标相同;P3(-a,-b)P(a,b)5 、点 P(a,b) 关于 x 轴、 y 轴、原点对称点的坐标 :xyOP1(a,-b)P2(-a,b)6 、点 P(a,b) 到 x 轴的距离为 , 到 y 轴的距离为 .ab 引例 : 如图是某地一天内的气温变化图.(6,-1)(3,-3)(10,2)(14,5)图像上每一个点的坐标 (t,T) 表示时间为 t 时的气温是 T.一般来说 , 函数的图象是由直角坐标系中的一系列点组成 . 在图象上每一点的坐标 (x,y) 中 , 横坐标 x 表示自变量的某一取值 , 纵坐标 y 表示与它对应的函数值 .例 1 画出函数 的图象 .212yx分析 : 函数图象上的点一般来说有无数多个 , 要把每个点都作出来得到函数图象很困难 , 甚至是不可能的 . 所以我们常作出函数图象上的一部分点 , 然后用光滑的曲线把这些点连接起来得到函数的图象 .请同学们想一想 , 怎么才能得到图象上的一部分点呢 ?为此 , 我们首先要取一些自变量 x 的值 , 求出对应的函数值 y, 那么以 (x,y) 为坐标的点就是函数图象上的点 . 为了表达方便 , 我们可以列表来表示 x 和 y 的对应关系 .解 : 取自变量的一些值 , 例如 -3 、 -2 、 -1 、 0 、 1 、 2 、 3, 计算出对应的函数值 , 列表表示:例 1 画出函数 的图象 .212yx4.520.500.524.5x … -3 -2 -1 0 1 2 3 … y … …xo-4-3-2-112345-5y12345大家自己总结一下 ,看看我们在做这个函...