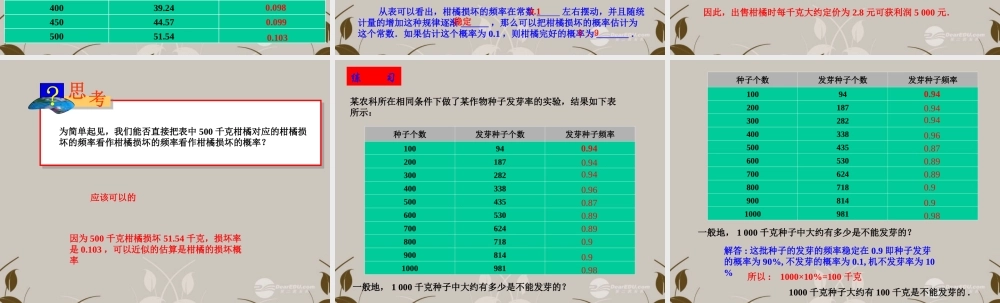
当试验的可能结果有很多并且各种结果发生的可能性相等时,我们可以用 的方式得出概率,当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,我们一般还要通过统计频率来估计概率.nm P (A) = 在同样条件下,大量重复试验时,根据一个随机事件发生的频率所逐 渐稳定到的常数,可以估计这个事件发生的概率.由频率可以估计概率是由瑞士数学家雅各布 · 伯努利( 1654-1705 )最早阐明的,因而他被公认为是概率论的先驱之一.一 . 利用频率估计概率 问题 1 某林业部门要考查某种幼树在一定条件的移植的成活率,应采用什么具体做法?下表是一张模拟的统计表,请补出表中的空缺,并完成表后的填空.移植总数( n )成活率( m )成活的频率( )1080.8050472702350.871400369750662150013350.890350032030.915700063359000807314000126280.902nm二 . 思考解答0.940.9230.8830.9050.897从表可以发现 , 幼树移植成活的频率在 _________ 左右摆动 ,并且随着统计数据的增加 , 这种规律愈加越明显 , 所以估计幼树移植成活率的概率为 ________0.602126281400080739000633570000.915320335000.890133515006627503694000.87123527047500.80810成活的频率( )成活率( m )移植总数( n )nm0.940.9230.8830.9050.8970.990%问题 2 某水果公司以 2 元 / 千克的成本新进了 10 000 千克的柑橘,如果公司希望这些柑橘能够获得利润 5 000 元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.51.5450044.5745039.2440035.3235030.9330024.2525019.4220015.151500.10510.51000.1105.5050柑橘损坏的频率( )损坏柑橘质量( m ) / 千克柑橘总质量( n ) / 千克nm0.1010.0970.0970.1030.1010.0980.0990.10351.5450044.5745039.2440035.3235030.9330024.2525019.4220015.151500.10510.51000.1105.5050柑橘损坏的频率( )损坏柑橘质量( m ) / 千克柑橘总质量( n ) / 千克nm0.1010.0970.0970.1030.1010.0980.0990.103 从表可以看出,柑橘损坏的频率在常数 _____ 左右摆动,并且随统计量的增加这种规律逐渐 ______ ,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为 0.1 ,则柑橘完好的概率为 _______...