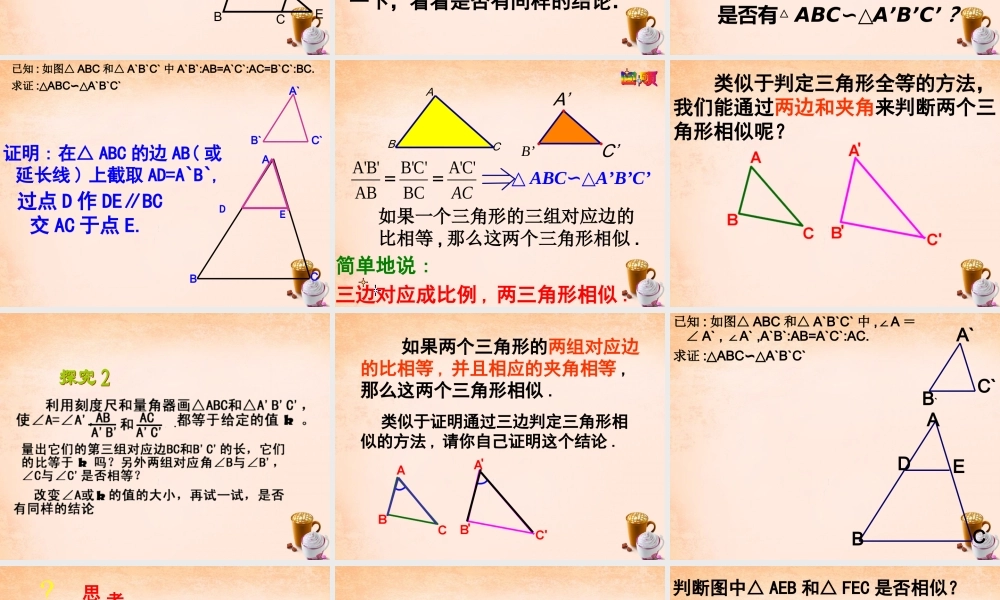
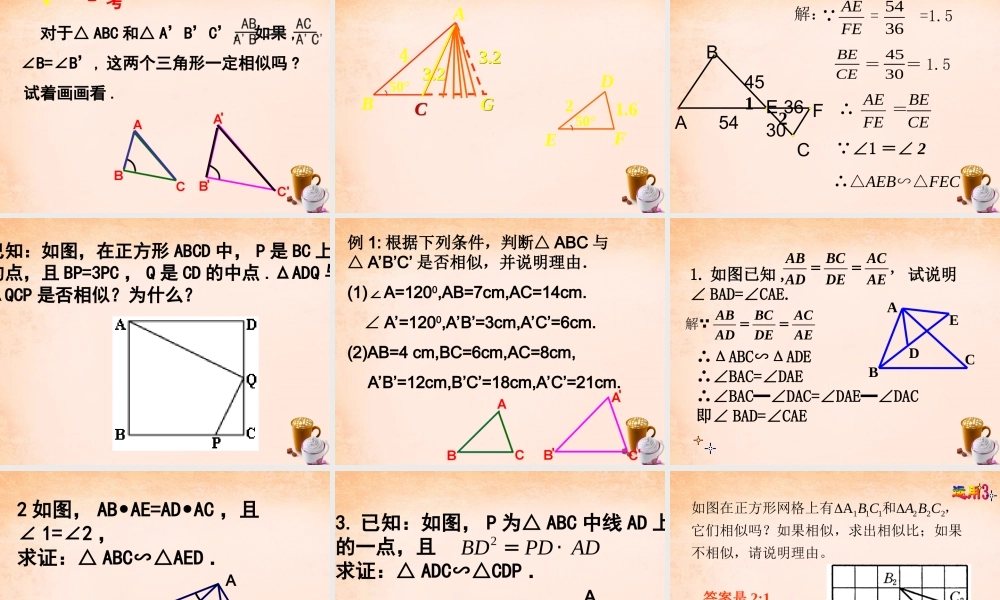
1. 对应角 _______, 对应边——————的两个三角形 ,叫做相似三角形 .相等成比例2. 相似三角形的——————— , 各对应边——————。对应角相等成比例3. 如何识别两三角形是否相似 ? DE BC∥ ∴ △ ADE ABC∽△ 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。DEOBCABCDE1. 如图,在△ ABC中, DG EH FI BC∥∥∥,( 1 )请找出图中所有的相似三角形;( 2 )如果 AD=1 , DB=3 ,那么 DG : BC=_____ 。ABCDEFGHI△ADG∽△AEH∽△AFI∽△ABC1 :4练习: 2. 如图,△ ABC 中, DE∥BC , GF∥AB , DE 、GF交于点O,则图中与△ ABC相似的三角形共有多少个 ? 请你写出来 .解: 与△ ABC 相似的三角形有 3 个 : △A DE △ GFC △ GOEABCDEFGOABCDEF3 、如图, E 是平行四边形 ABCD 的边BC 的延长线上一点,连接 AE 交 CD 于 F,则图中共有相似三角形 _______ 对3 任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的K倍,度量这两个三角的对应角,它们相等吗?这两个三角形相似吗?相互交流一下,看看是否有同样的结论.三边对应成比例A'B'B'C'A'C'ABBCAC== 是否有△ ABC∽△A’B’C’ ?ABCC’B’A’已知 : 如图△ ABC 和△ A`B`C` 中 A`B`:AB=A`C`:AC=B`C`:BC.求证 : ABCA`B`C`△∽△证明 : 在△ ABC 的边 AB( 或延长线 ) 上截取 AD=A`B`, A`B`C`ABCDE过点 D 作 DE∥BC交 AC 于点 E.ABCC’B’A’A'B'B'C'A'C'ABBCAC==△ ABC∽△A’B’C’简单地说 :三边对应成比例 , 两三角形相似 .如果一个三角形的三组对应边的比相等 , 那么这两个三角形相似 . 类似于判定三角形全等的方法,我们能通过两边和夹角来判断两个三角形相似呢? 如果两个三角形的两组对应边的比相等 , 并且相应的夹角相等 ,那么这两个三角形相似 . 类似于证明通过三边判定三角形相似的方法 , 请你自己证明这个结论 .已知 : 如图△ ABC 和△ A`B`C` 中 ,A∠=∠ A` , A` ,A`B`:AB=A`C`:AC.∠求证 : ABCA`B`C`△∽△A`B`C`ABCED思 考? 对于△ ABC 和△ A’B’C’, 如果 , ∠B=∠B’, 这两个三角形一定相似吗 ? 试着画画看 .3.23.23.23.2GGCC50°)4AB21.650°)EDF = =1.5FEAE3654判断图中△ AEB 和△ FEC 是否相似? 解:∴...