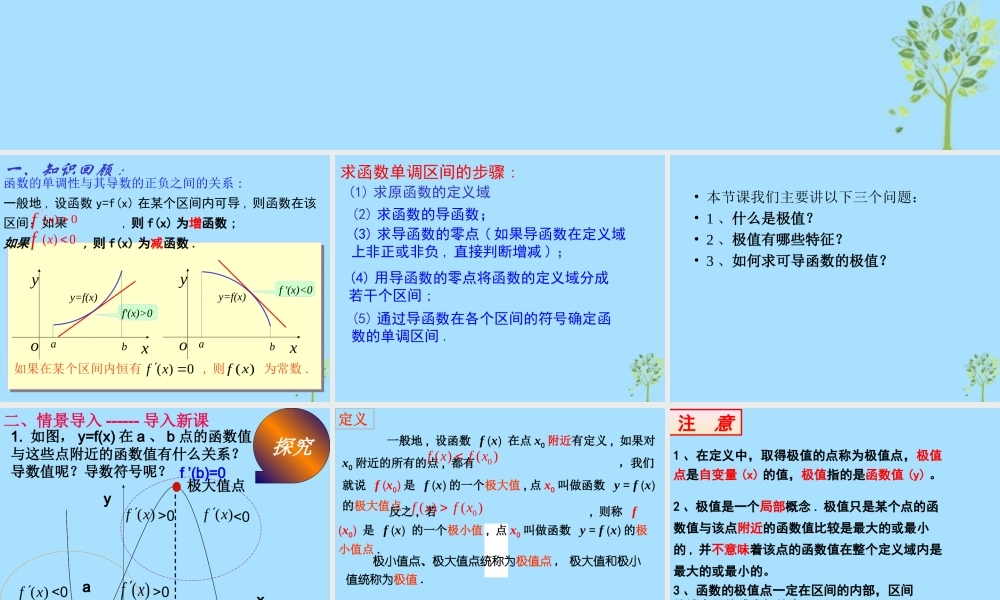
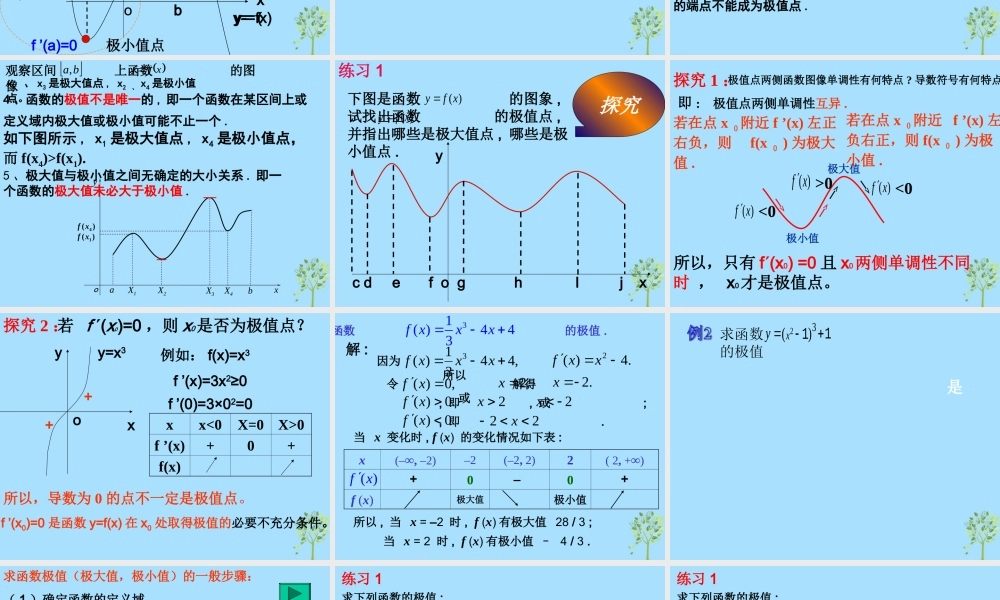
极值极值aby=f(x)xoyy=f(x)xoyabf'(x)>0f '(x)<0函数的单调性与其导数的正负之间的关系 :一、知识回顾 :如果在某个区间内恒有 , 则 为常数 .0)( xf)(xf一般地 , 设函数 y=f(x) 在某个区间内可导 , 则函数在该区间:如果 , 则 f(x) 为增函数 ;如果 , 则 f(x) 为减函数 . '( )0xf'( )0xf求函数单调区间的步骤 :(2) 求函数的导函数;(3) 求导函数的零点 ( 如果导函数在定义域上非正或非负 , 直接判断增减 ) ;(4) 用导函数的零点将函数的定义域分成若干个区间 ;(5) 通过导函数在各个区间的符号确定函数的单调区间 .(1) 求原函数的定义域• 本节课我们主要讲以下三个问题:• 1 、什么是极值?• 2 、极值有哪些特征?• 3 、如何求可导函数的极值?二、情景导入 ------ 导入新课1. 如图, y=f(x) 在 a 、 b 点的函数值与这些点附近的函数值有什么关系?导数值呢?导数符号呢?探究xyoaby-=fx)xyoaby= ( ( )fx( )fx( )f x>0<0<0( )fx>0极小值点极大值点f ’(a)=0f ’(b)=0定义 一般地 , 设函数 f (x) 在点 x0 附近有定义 , 如果对x0 附近的所有的点 , 都有 ,我们就说 f (x0) 是 f (x) 的一个极大值 , 点 x0 叫做函数 y = f (x)的极大值点 .0( )()f xf x 反之 , 若 , 则称 f (x0) 是 f (x) 的一个极小值 , 点 x0 叫做函数 y = f (x) 的极小值点 .0( )()f xf x 极小值点、极大值点统称为极值点 , 极大值和极小值统称为极值 .1 、在定义中,取得极值的点称为极值点,极值点是自变量 (x) 的值,极值指的是函数值 (y) 。注 意2 、极值是一个局部概念 . 极值只是某个点的函数值与该点附近的函数值比较是最大的或最小的 , 并不意味着该点的函数值在整个定义域内是最大的或最小的。3 、函数的极值点一定在区间的内部,区间的端点不能成为极值点 .oaX1X2X3X4bxy)(4xf)(1xf如下图所示 , x1 是极大值点 , x4 是极小值点,而 f(x4)>f(x1).5 、极大值与极小值之间无确定的大小关系 . 即一个函数的极大值未必大于极小值 .4 、函数的极值不是唯一的 , 即一个函数在某区间上或定义域内极大值或极小值可能不止一个 .x1 、 x3 是极大值点 , x2 、 x4 是极小值点。观察区间 上函数 的图像ba, xfy 练习 1探究下图是函数 的图象 , 试找出函数 的极值点 , ...