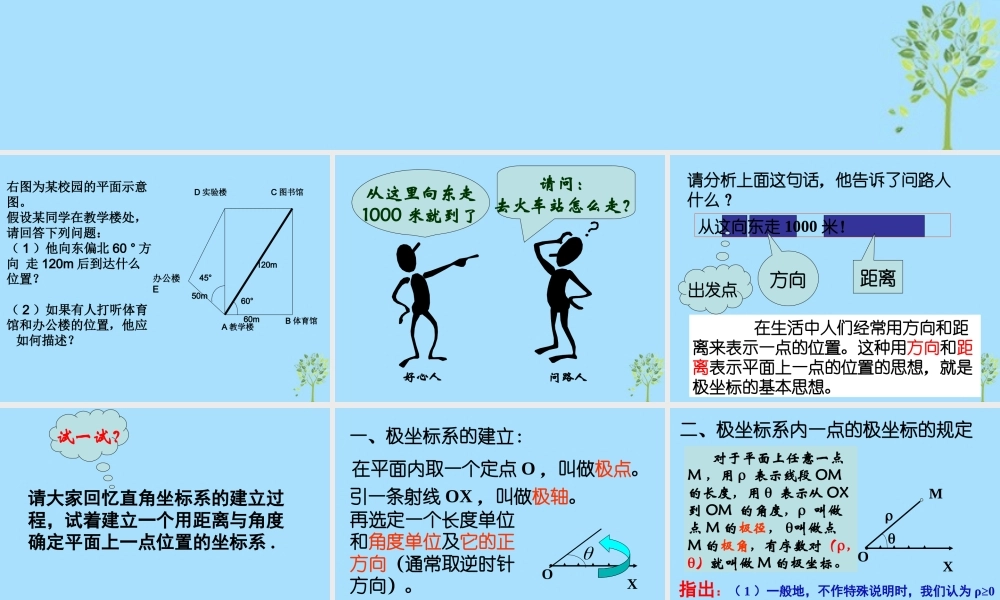
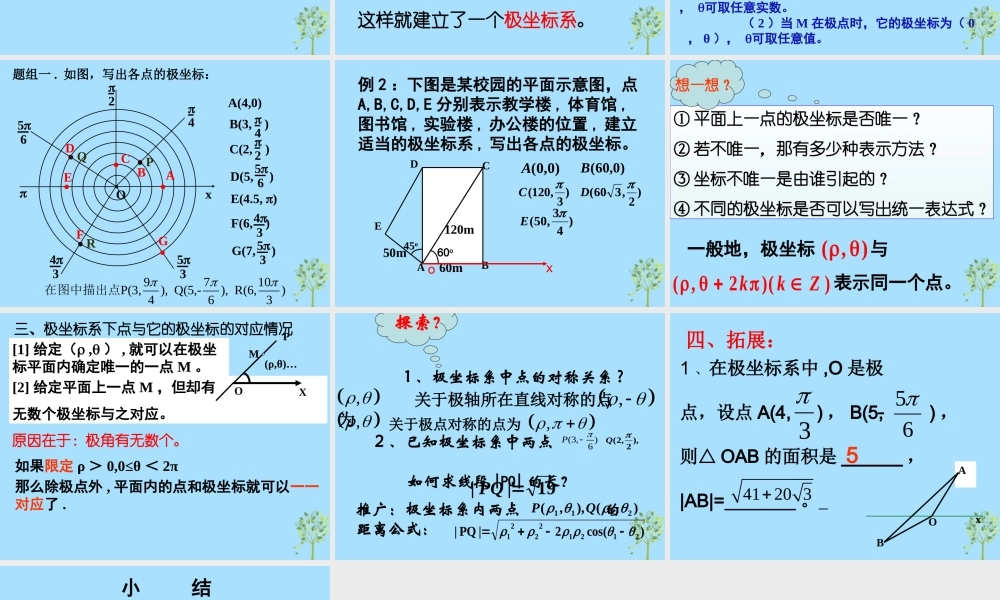
极坐标系极坐标系60°60m45°C 图书馆D 实验楼50m120mB 体育馆A 教学楼右图为某校园的平面示意图。假设某同学在教学楼处,请回答下列问题:( 1 )他向东偏北 60 ° 方向 走 120m 后到达什么位置?( 2 )如果有人打听体育馆和办公楼的位置,他应 如何描述?办公楼E 从这里向东走1000 米就到了请问:去火车站怎么走?问路人好心人请分析上面这句话,他告诉了问路人什么?从这向东走 1000 米!出发点方向距离 在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。请大家回忆直角坐标系的建立过程,试着建立一个用距离与角度确定平面上一点位置的坐标系 . 试一试?一、极坐标系的建立:在平面内取一个定点 O ,叫做极点。引一条射线 OX ,叫做极轴。再选定一个长度单位和角度单位及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。XO二、极坐标系内一点的极坐标的规定XOM 对于平面上任意一点M ,用 表示线段 OM的长度,用 表示从 OX到 OM 的角度, 叫做点 M 的极径, 叫做点M 的极角,有序数对(,)就叫做 M 的极坐标。指出:( 1 )一般地,不作特殊说明时,我们认为 ρ≥0, 可取任意实数。 ( 2 )当 M 在极点时,它的极坐标为( 0, θ ), 可取任意值。题组一 . 如图,写出各点的极坐标:。Ox42564353A•B•C•D•E•F•G•A(4,0)B(3, )4C(2, )2D(5, )56E(4.5, )F(6, )43G(7, )539710P(3,), Q(5,-), R(6,)463在图中描出点P•Q•R•例 2 :下图是某校园的平面示意图,点 A,B,C,D,E 分别表示教学楼 , 体育馆 ,图书馆 , 实验楼 , 办公楼的位置 , 建立适当的极坐标系 , 写出各点的极坐标。50mBDECA60m120m45o60oOX)0,0(A)0,60(B)3,120(C)2,360(D)43,50(E① 平面上一点的极坐标是否唯一?② 若不唯一,那有多少种表示方法?③ 坐标不唯一是由谁引起的?④ 不同的极坐标是否可以写出统一表达式?想一想?一般地,极坐标 与 表示同一个点。),())(2,(Zkk三、极坐标系下点与它的极坐标的对应情况[1] 给定( , ) , 就可以在极坐标平面内确定唯一的一点 M 。[2] 给定平面上一点 M ,但却有无数个极坐标与之对应。原因在于:极角有无数个。OXPM(ρ,θ)…如果限定 ρ > 0,0≤θ < ...