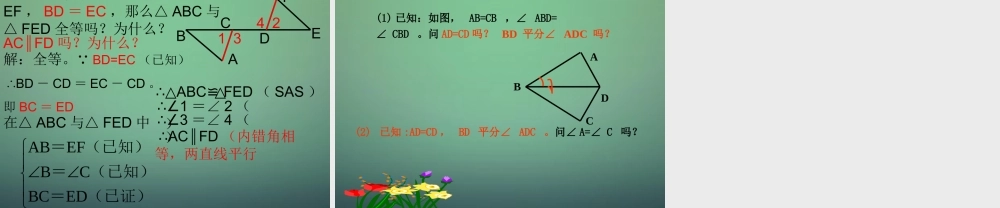
1 三角 2 三边 : SSS 4 两边一角3 两角一边 : ASA AAS 三角形全等满足三个条件时,有可能的 4 种情况复习创设情景创设情景 因铺设电线的需要,要在池塘两侧 A 、 B 处各埋设一根电线杆(如图),因无法直接量出 A 、 B两点的距离,现有一足够的米尺。怎样测出 A 、 B 两杆之间的距离呢?AB 画△ ABC ,使它的两边长 AB=6cm, BC=4cm, ∠B=60 度 . 把你所画的三角形剪下来与小组成员的三角形进行 比较,它们能互相重合吗?探究 1 三角形全等判定方法三角形全等判定方法 ::用符号语言表达为:在△ ABC 与△ DEF 中AB=DE∠B=E∠BC=EF∴△ABCDEF≌△( SAS )ABCDEF 两边和它们的夹角对应相等的两个三角形全等 .简写成“边角边”或““ SASSAS”” 例 1 如图, AC=BD ,∠ CAB= DBA∠,你能判断 BC=AD 吗?说明理由。ABCD理由 : 在△ ABC 与△ BAD中 AC=BD ∠CAB=DBA∠ AB=BA∴△ABCBAD≌△( SAS )( 已知 )( 已知 )( 公共边 ) 例题欣赏∴BC=AD(全等三角形的对应边相等)解: BA=AD 如图,在△ AEC 和△ ADB 中,已知 AE=AD , AC=AB ,请说明△ AEC A≌ △DB 的理由 .AEBDCAE=AD ( 已知 ) = ( )AC = AB ( 已知 )SAS解:在△ AEC 和△ ADB中 ∴ △AECADB≌△( )∠A∠A 公共角练一练探究 2 画一个△ ABC ,使∠ B=45° , AB=5cm , AC=4cm ,这两个三角形全等吗?45°5cm4cmABC(图①).45°4cm5cmABC(图②) 有两边和其中一边的对角对应相等的两个三角形不一定全等 . 小明的设计方案:先在池塘旁取一个能直接到达 A和 B 处的点 C ,连结 AC 并延长至 D 点,使 AC=DC ,连结 BC 并延长至 E 点,使 BC=EC ,连结 DE ,用米尺测出DE 的长,这个长度就等于 A , B 两点的距离。请你说明理由。AC=DC∠ACB=DCE∠ BC=EC ∴△ACBDCE≌△∴AB=DE在△ ACB 和△ DCE 中问题回顾 现在你知道哪些三角形全等的判定方法?SSS. ASA. AAS. SAS. 我思我能行注意:“边边角”不能判定两个三角形全等1. 若 AB=AC ,则添加什么条件可得△ ABD ACD?≌ △△ABD △ ACD△AB=ACABDC∠BAD= CAD∠SA SAD=ADBD=CDS已知:如图 AB=AC,AD=AE,BAC=DA∠∠E求证: ∠ B=C∠ABDCE再见 !!!2. 如图,要证△ ACB ADB ≌ △,至少选用哪些条件可ABCD△ACB ADB≌ △SAS证得△ ACB ADB≌ △AB=AB ...