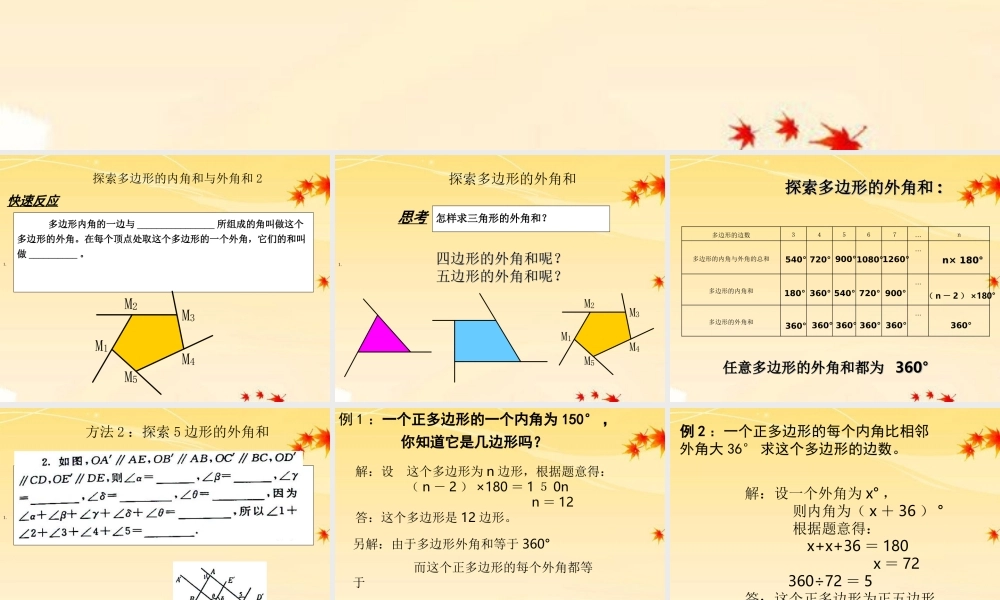
9.2 多边形的内角和与外角和(第二课时)华东师大版七年级(下册)探索多边形的内角和与外角和 2 多边形内角的一边与 ________________ 所组成的角叫做这个多边形的外角。在每个顶点处取这个多边形的一个外角,它们的和叫做 __________ 。 快速反应 1. M1M5M4M3M2探索多边形的外角和怎样求三角形的外角和?1. M1M5M4M3M2思考 四边形的外角和呢?四边形的外角和呢?五边形的外角和呢?五边形的外角和呢?探索多边形的外角和探索多边形的外角和 ::任意多边形的外角和都为 任意多边形的外角和都为 360°360°多边形的边数34567…n多边形的内角与外角的总和…多边形的内角和…多边形的外角和…540° 720° 900° 1080° 1260° 180° 360° 540° 720° 900° 360° 360° 360° 360° 360° n× 180°n× 180°( n - 2 ) ×180° 360° 方法 2 :探索 5 边形的外角和2 、1. 例 1 :一个正多边形的一个内角为 150° , 你知道它是几边形吗? 解:设 这个多边形为 n 边形,根据题意得: ( n - 2 ) ×180 = 1 5 0n n = 12答:这个多边形是 12 边形。另解:由于多边形外角和等于 360° 而这个正多边形的每个外角都等于 180° - 150° = 30° , 所以这个正 多边形的边数等于 360°÷30° = 12 。例 2 :一个正多边形的每个内角比相邻外角大 36° 求这个多边形的边数。 解:设一个外角为 x° , 则内角为( x + 36 ) ° 根据题意得: x+x+36 = 180 x = 72 360÷72 = 5答:这个正多边形为正五边形。1 、有一个正多边形的外角是 60° ,那么该正多边形是正 ___________ 边形。 快速反应 2 、有一个多边形的内角和是它的外角和的 3 倍,那么该多边形的边数是 ____________. 1 、一个多边形的每个内角都比邻外角的 3 倍还多 20 度,求这个多边形的边数。 自主学习自主学习 •2 、如果一个多边形的每一个外角都相等,并且小于 45 度,那么这个多边形的边数最少是多少? 3 、已知四边形四个外角的度数之比分别为 8 :6 : 3 : 7 。求四边形四个内角的度数分别是多少? 开动脑筋若多边形的所有内角与它的一个外角的和为 600°, 求这个多边形的边数和内角和 .3 、如图,∠ M1+∠M2+∠M3……+∠M6=_______ 。1. M1M6M5M4M3M2自主学习自主学习 4 、如图是一个五角星的每个角剪去一部...