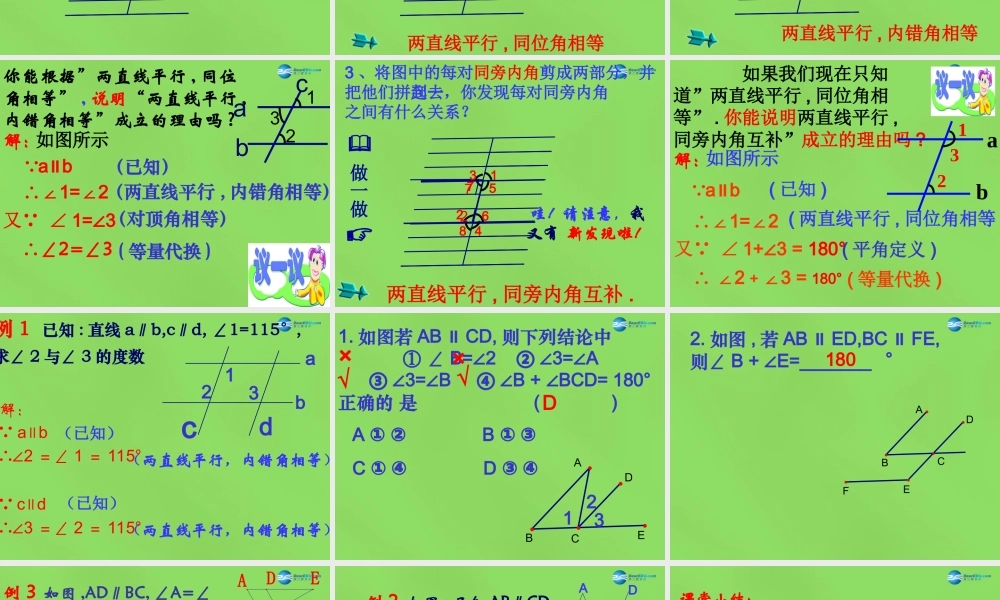
ABCDMN1 、在练习本上画两条平行线 AB 、 CD ,再画直线 MN 与直线AB 、 CD 相交2 、指出图中同位角、内错角、同旁内角13682574(如下图)( )复习与回顾( 1 ) ∠ =_∠__ ∴ ab∥( )( 2 ) ∠ = ∠ ∴ ab∥1224同位角相等,两直线平行内错角相等,两直线平行cb4321a( )( 3 ) ∠ +∠ =180° ∴ ab∥23同旁内角互补,两直线平行复习与回顾4321acb7256318 42 、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?做一做2 、将上图按照如下方式剪开,并分别把剪开得到的每对同位角重叠,你发现了什么?做一做7256两直线平行 , 同位角相等哇!我有发现啦!318 42 、将上图按照如下方式剪开,并分别把剪开得到的每对 重叠,你发现了什么?做一做8 4725631两直线平行 , 内错角相等哇!我又知道啦!内错角你能根据”两直线平行 , 同位角相等” , 说明“两直线平行 ,内错角相等”成立的理由吗 ?abc123解: a b∥∴∠1=2∠如图所示又 ∠ 1= 3∠ (对顶角相等)(已知)(两直线平行 , 内错角相等)∴∠2=∠3 ( 等量代换 )做一做72563 、将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?两直线平行 , 同旁内角互补 .哇!请注意,我又有 新发现啦!7318 42 如果我们现在只知道”两直线平行 , 同位角相等” . 你能说明两直线平行 ,同旁内角互补”成立的理由吗 ? ∴ ∠2 + 3 = ∠180° 解:如图所示1a32b a b∥( 已知 )∴∠1=2∠( 两直线平行 , 同位角相等 )又 ∠ 1+ 3 = ∠180° ( 平角定义 )( 等量代换 )例 1 已知 : 直线 a∥b,c∥d, ∠1=115°,求∠ 2 与∠ 3 的度数解: a b∥∴∠2 =∠ 1 = 115° c d∥∴∠3 =∠ 2 = 115°(两直线平行,内错角相等) (已知)(已知)(两直线平行,内错角相等) 123abcd1. 如图若 AB CD,∥则下列结论中 ① ∠ B= 2 3= A ∠② ∠∠ 3= B B + BCD= 180°③ ∠∠④ ∠∠正确的 是 ( )A B ① ②① ③C D ① ④③ ④DABECD123×√×√2. 如图 , 若 AB ED,BC FE,∥∥则∠ B + E=_______∠ABCDEF°180例 3 如图 ,AD∥BC, ∠A=∠C. 试说明 AB∥DCAEFCBD( 同位角相等 , 两直线平行 )解 : AD BC∥( 已知 )∴∠C=CDE∠( ...