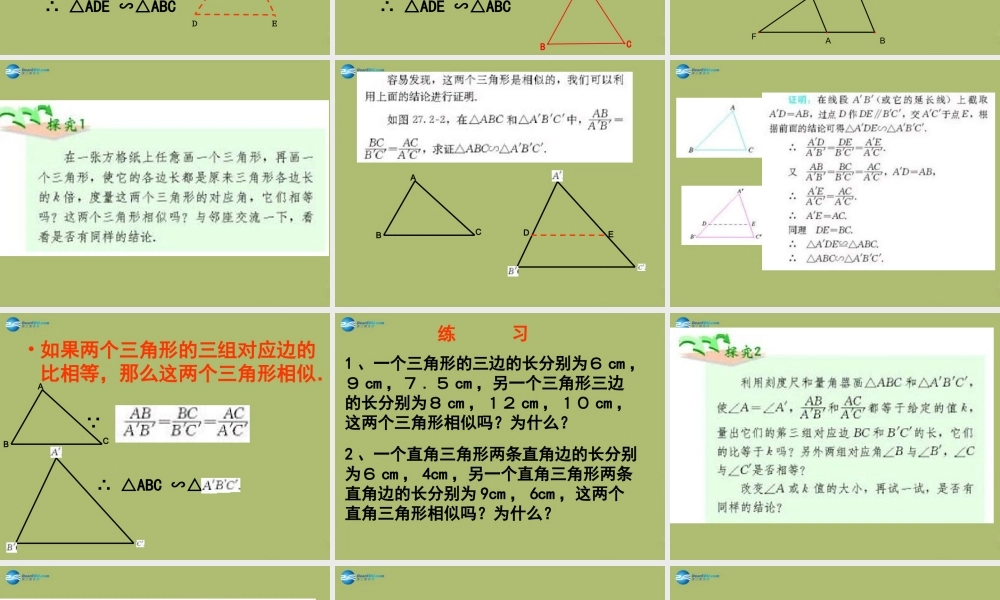
相似三角形的判定(1)EDCBAFEDCBA基本定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∵ DE∥BC∴ △ADE ∽△ABC思考一:如图,平行于三角形一边的直线和其他两边的延长线相交,所构成的三角形与原三角形相似吗?ABCDE∵ DE∥BC∴ △ADE ∽△ABC• 思考二:如图,平行于三角形一边的直线和其他两边的反向延长线相交,所构成的三角形与原三角形相似吗?EDCBA∵ DE∥BC∴ △ADE ∽△ABC1、如图,DE∥FG∥BC,图中共有相似三角形( )对。ABCGEDF2 、如图在平行四边形 ABCD 中, E 为 AD上一点,连结 CE 并延长交 BA 的延长线于点 F ,请找出相似的三角形并表示出来。FEDCBAABCDE• 如果两个三角形的三组对应边的比相等,那么这两个三角形相似.∵∴ △ABC ∽△ABC1 、一个三角形的三边的长分别为6 cm ,9 cm ,7 . 5 cm ,另一个三角形三边的长分别为8 cm ,12 cm ,10 cm ,这两个三角形相似吗?为什么?练 习2 、一个直角三角形两条直角边的长分别为6 cm , 4cm ,另一个直角三角形两条直角边的长分别为 9cm , 6cm ,这两个直角三角形相似吗?为什么? 如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.2 、一个直角三角形两条直角边的长分别为6 cm , 4cm ,另一个直角三角形两条直角边的长分别为 9cm , 6cm ,这两个直角三角形相似吗?为什么?你可以用几种方法进行判断呢?3、要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边为2,它的另外两条边长应当是多少?你有几个答案? 如图,DE与△ABC的边AB,AC分别相交于D,E两点,AE=2 cm ,AC=3 cm ,AD=2 .4 cm ,AB=3 . 6 cm ,DE=4/3 cm ,则BC= 。ADECB• 如图 , 在□ ABCD 中 ,AB=10,AD=6,E 是AD 的中点 , 在 AB 上取一点 F, 使△ CBF与△ CDE 相似 , 则 BF 的长是 :A 、 5 B 、 8.2 C 、 6.4 D 、 1.8FEDCBA• 如图 , 在□ ABCD 中, EF AB∥,DE : EA=2 : 3 , EF=4 ,则CD 的长为( )FEDCBA• 在△ABC中, AB=9 , AC=12 , BC=18 ,D 为 AC 上的一点, DC=2AC/3 ,在 AB 上取一点 E ,得到△A DE ,,若图中两个三角形相似时,则 DE 长为: 。EDCBAEDCBA