广东省高考数学二轮专题复习 专题7 第35课时 选择题的解法(二)课件 理 新人教版 课件VIP免费

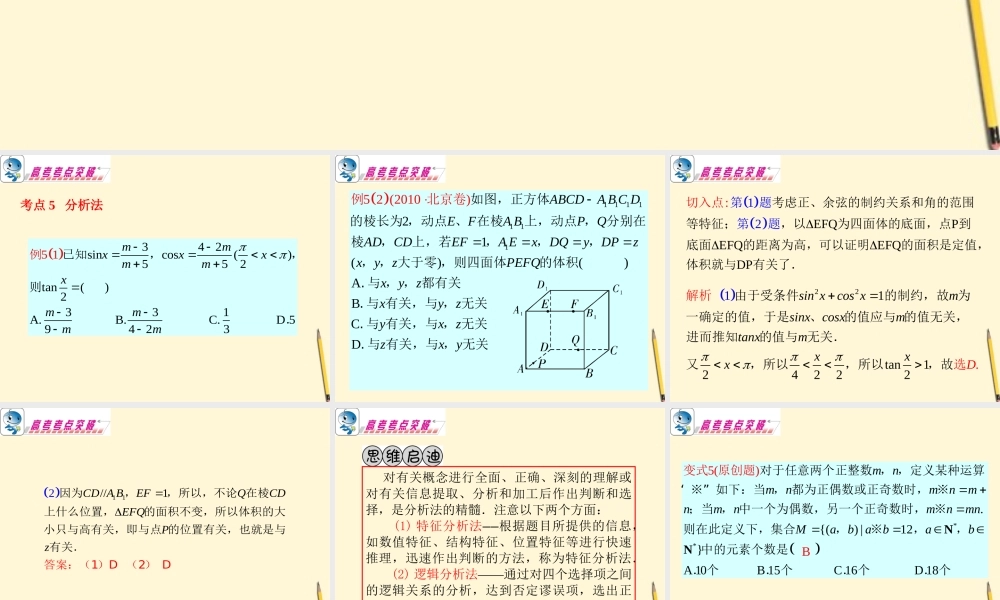
专题七 客观题的解法 342sincos()552tan()2331A. B. C. D 59435 12mmxxxmmxmmmm已知，，则 例 ．考点 5 分析法 11111115 2 (2010)21()()ABCDABCDA B C DEFA BPQADCDEFA ExDQyDPzxyzPEFQxyzxyzyxzzxy如图，正方体的棱长为 ，动点 、 在棱上，动点 ， 分别在棱，上，若，，，， ， 大于零 ，则四面体的体积 . 与 ， ， 都有关 . 与 有关，与 ， 无关. 与 有关，与 ， 无关 . 与 有关，例卷与京，北无关  EFQ:PEFQEFQDP12考虑正、余弦的制约关系和角的范围等特征；，以为四面体的底面第题，点 到底面的距离为高，可以证明的面积是定值，体积切入点就与第题有关了． 221tan124222.1sin xcos xmsinxcosxmtanxmxxxD由于受条件的制约，故 为一确定的值，于是、的值应与 的值无关，进而推知的值与 无关．又，所以，所以解，故析 选 11//12CD A BEFQCDEFQPz因为，，所以，不论 在棱上什么位置，的面积不变，所以体积的大小只与高有关，即与点 的位置有关，也就答案：（1）D （是与有关．2） D 对有关概念进行全面、正确、深刻的理解或对有关信息提取、分析和加工后作出判断和选择，是分析法的精髓．注意以下两个方面： (1) 特征分析法——根据题目所提供的信息，如数值特征、结构特征、位置特征等进行快速推理，迅速作出判断的方法，称为特征分析法． (2) 逻辑分析法——通过对四个选择项之间的逻辑关系的分析，达到否定谬误项，选出正 确项的方法，称为逻辑分析法．**.{() |12} A 10 B 15 C 16 (851)DmnmnmnmnmnmnmnMabababNN对于任意两个正整数 ， ，定义某种运算“ ※” 如下：当 ， 都为正偶数或正奇数时， ※；当 ， 中一个为偶数，另一个正奇数时， ※则在此定义下，集合，※，，中的元素个数是．个． 个变式 原创． 个．题个B121212121 112 103948576616,62 5 1 11ababmnmnabmnmnabab        从定义出发，抓住 ， 的奇偶性对实行分拆是解决本题的关键，当 ， 同奇偶时，根据 ※将分拆两个同奇偶数的和，当 ， 一奇一偶时，根据 ※将分拆一个奇数与一个偶数的积，再算其组数即可． 若 ， 同奇偶，有，前面的每种可以交换位置，最后一种只有 个点，这时有； 解析...