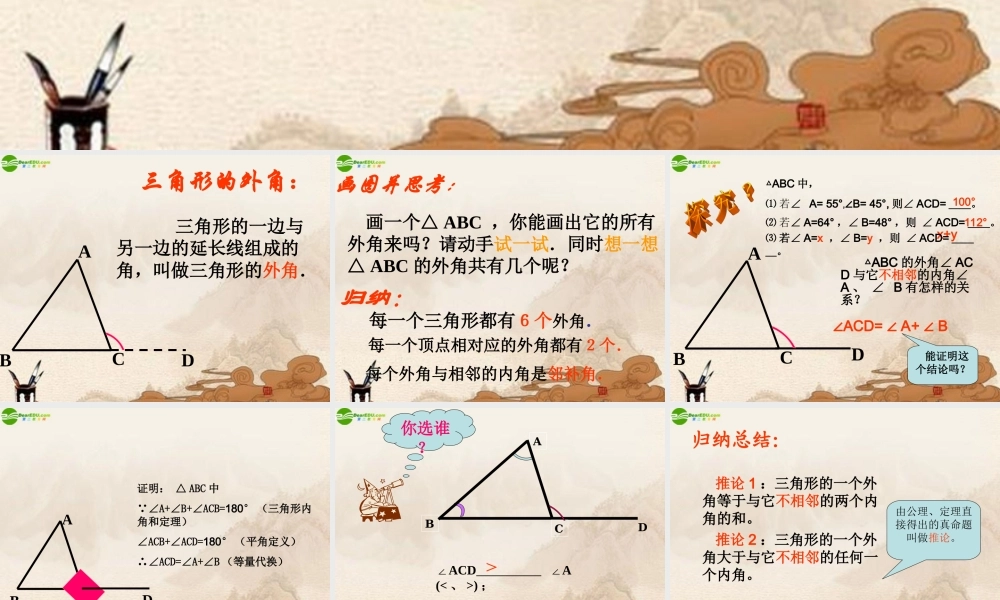
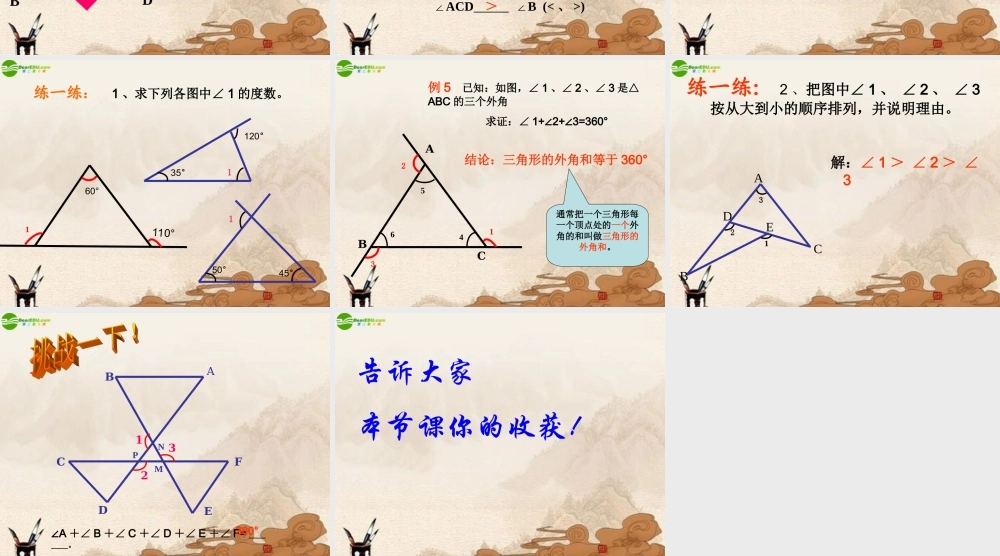
14.2 命题与证明 —三角形的外角ABCD三角形的外角: 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.画图并思考: 画一个△ ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ ABC 的外角共有几个呢?归纳: 每一个三角形都有6个外角.每一个顶点相对应的外角都有2个.每个外角与相邻的内角是邻补角.ABC △ABC 的外角∠ ACD 与它不相邻的内角∠ A 、 ∠ B 有怎样的关系?D△ABC 中,⑴ 若∠ A= 55°, B= 45°,∠则∠ ACD= __。∠ACD= A+ B∠∠100°112°x+y⑵ 若∠ A=64° ,∠ B=48° ,则 ∠ ACD= __。⑶ 若∠ A=x ,∠ B=y ,则 ∠ ACD= ___。 能证明这个结论吗?ABCD证明: △ ABC 中∵∠A+∠B+∠ACB=180° (三角形内角和定理)∠ACB+∠ACD=180° (平角定义)∴∠ACD=∠A+∠B (等量代换)ACB∠ACD A ∠(< 、 >) ;∠ACD B (<∠、 >)你选谁 ?D>>归纳总结: 推论 1 :三角形的一个外角等于与它不相邻的两个内角的和。 推论 2 :三角形的一个外角大于与它不相邻的任何一个内角。由公理、定理直接得出的真命题叫做推论。 160°110°练一练: 1 、求下列各图中∠ 1 的度数。50° 45° 1 35° 120° 1 321ABC564例 5 已知:如图,∠ 1 、∠ 2 、∠ 3 是△ABC 的三个外角 求证:∠ 1+ 2+ 3=360°∠∠结论:三角形的外角和等于 360°通常把一个三角形每一个顶点处的一个外角的和叫做三角形的外角和。练一练: 2 、把图中∠ 1 、 ∠ 2 、 ∠ 3按从大到小的顺序排列,并说明理由。解:∠ 1 > ∠ 2 > ∠3 321ABCDE123BACPNMDEF∠A +∠ B +∠ C +∠ D +∠ E +∠ F= ____。360°告诉大家本节课你的收获!