九年级数学相似三角形的性质及应用课件 新浙教版 课件VIP免费

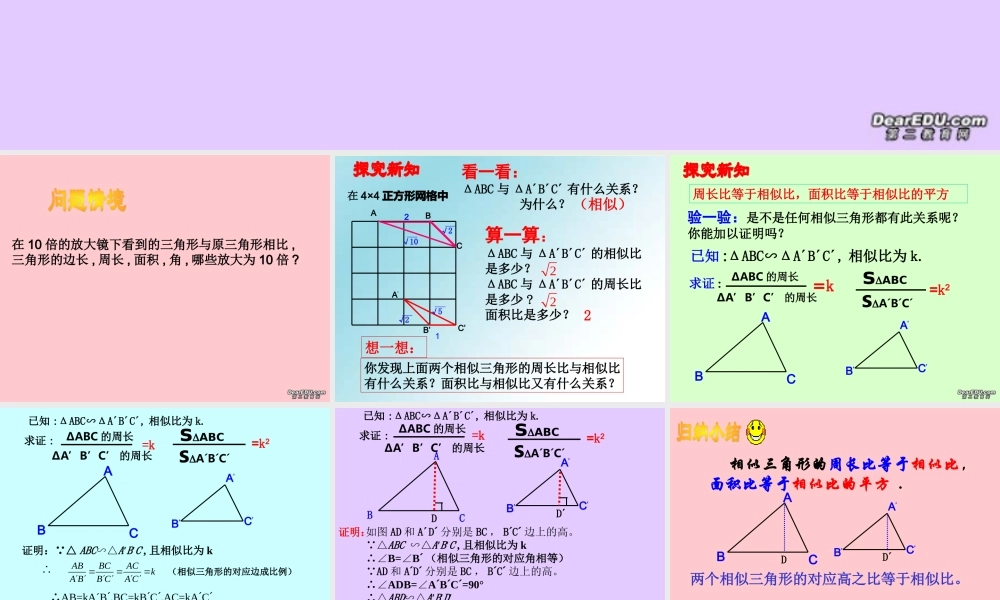
在 10 倍的放大镜下看到的三角形与原三角形相比 ,三角形的边长 , 周长 , 面积 , 角 , 哪些放大为 10 倍 ?算一算：ΔABC 与 ΔA´B´C´ 的相似比是多少？ΔABC 与 ΔA´B´C´ 的周长比是多少 ?面积比是多少？在 4×4 正方形网格中看一看：ΔABC 与 ΔA´B´C´ 有什么关系？ 为什么？ 想一想：你发现上面两个相似三角形的周长比与相似比有什么关系？面积比与相似比又有什么关系？（相似）2√102√21√5√2ABCA’C’B’22ABCA’B’C’已知 :ΔABC∽ΔA´B´C´, 相似比为 k.=k2求证 :ΔABC 的周长ΔA’B’C’ 的周长=ksABCsA´B´C´周长比等于相似比，面积比等于相似比的平方验一验：是不是任何相似三角形都有此关系呢？你能加以证明吗？证明： △ ABC∽△A′B′C′, 且相似比为 k∴ABBCACkA BB CA C   （相似三角形的对应边成比例）∴AB=kA´B´,BC=kB´C´,AC=kA´C´∴ABCABBCACkA BkB CkA CkA B CA BB CA CA BB CA C                的周长的周长ABCA’B’C’已知 :ΔABC∽ΔA´B´C´, 相似比为 k.=k2求证 :ΔABC 的周长ΔA’B’C’ 的周长=ksABCsA´B´C´如图 AD 和 A´D´ 分别是 BC ， B´C´ 边上的高。 △ABC ∽△A′B′C′, 且相似比为 k∴∠B=B∠ ´ （相似三角形的对应角相等） AD 和 A´D´ 分别是 BC ， B´C´ 边上的高。∴∠ADB=A∠ ´B´C´=90°∴△ABD∽△A′B′D′（有两个角对应相等的两个三角形相似）∴kBAABDAAD’‘’‘21212BCADABCBCADkkkA B CB CA DB CA D        的面积的面积证明：ABCA’B’C’已知 :ΔABC∽ΔA´B´C´, 相似比为 k.=k2求证 :ΔABC 的周长ΔA’B’C’ 的周长=ksABCsA´B´C´DD´ABCA’B’C’ 相似三角形的周长比等于相似比，面积比等于相似比的平方 .两个相似三角形的对应高之比等于相似比。类似地 , 相似三角形对应中线的比与对应角平分线的比也等于相似比。DD´ 在 10 倍的放大镜下看到的三角形与原三角形相比 ,三角形的边长 , 周长 , 面积 , 角 , 哪些放大为 10 倍 ?答 : 三角形的边长 , 周长放大为 10 倍 .三角形的面积放大为 100 倍 .三角形的角大小不变 .已知两个三角形相...