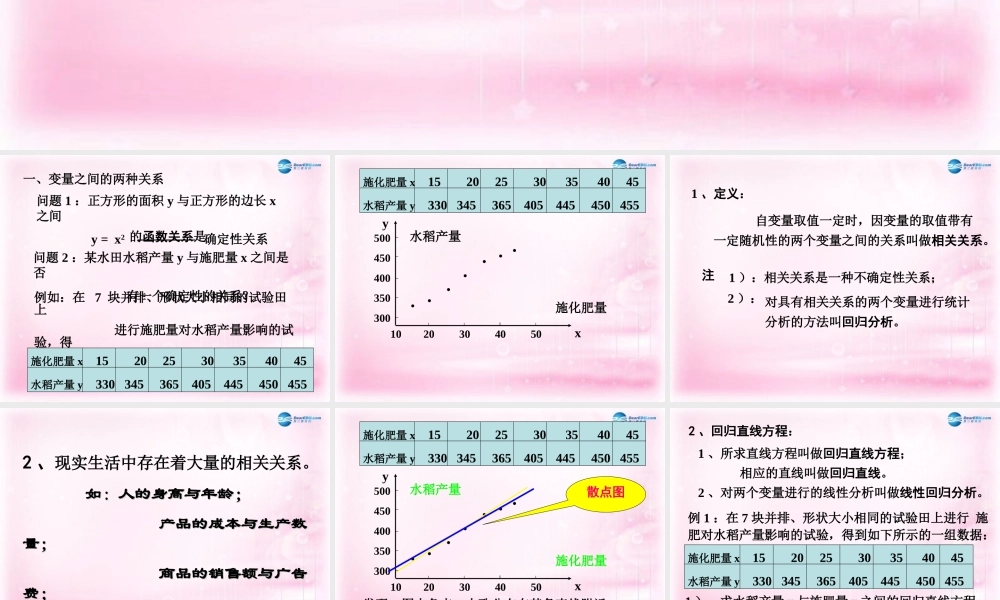
相关性问题 1 :正方形的面积 y 与正方形的边长 x之间 的函数关系是y = x2确定性关系问题 2 :某水田水稻产量 y 与施肥量 x 之间是否 有一个确定性的关系?例如:在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验,得 到如下所示的一组数据:施化肥量 x 15 20 25 30 35 40 45水稻产量 y 330 345 365 405 445 450 455一、变量之间的两种关系10 20 30 40 50500450400350300· · · · · · ·施化肥量 x 15 20 25 30 35 40 45水稻产量 y 330 345 365 405 445 450 455xy施化肥量水稻产量 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。1 、定义: 1 ):相关关系是一种不确定性关系;注对具有相关关系的两个变量进行统计分析的方法叫回归分析。2 ):2 、现实生活中存在着大量的相关关系。 如:人的身高与年龄;如:人的身高与年龄; 产品的成本与生产数产品的成本与生产数量;量; 商品的销售额与广告商品的销售额与广告费;费; 家庭的支出与收入。家庭的支出与收入。等等等等探索:水稻产量 y 与施肥量 x 之间大致有何规律?10 20 30 40 50500450400350300· · · · · · ·发现:图中各点,大致分布在某条直线附近。探索 2 :在这些点附近可画直线不止一条,哪条直线最能代表 x 与 y 之间的关系呢?施化肥量 x 15 20 25 30 35 40 45水稻产量 y 330 345 365 405 445 450 455xy散点图施化肥量水稻产量1 、所求直线方程叫做回归直线方程; 相应的直线叫做回归直线。2 、对两个变量进行的线性分析叫做线性回归分析。例 1 :在 7 块并排、形状大小相同的试验田上进行 施肥对水稻产量影响的试验,得到如下所示的一组数据:施化肥量 x 15 20 25 30 35 40 45水稻产量 y 330 345 365 405 445 450 4551 )、求水稻产量 y 与施肥量 x 之间的回归直线方程;2 )、估计当施肥量为 70 时水稻的产量是多少?2 、回归直线方程:i 1 2 3 4 5 6 7xi 15 20 25 30 35 40 45yi 330 345 365 405 445 450 455 xiyi 4950 6900 9125 12150 15575 18000 20475 x=30 y=399.3∑xi2=7000 ∑ yi2=1132725 ∑ xiyi=87175i=1i=177i=17b=(∑ xiyi – n x y)/(∑xi2 - n x 2) i=1 7 7 i=1=(87175-7×30×399.3)/(7000-...