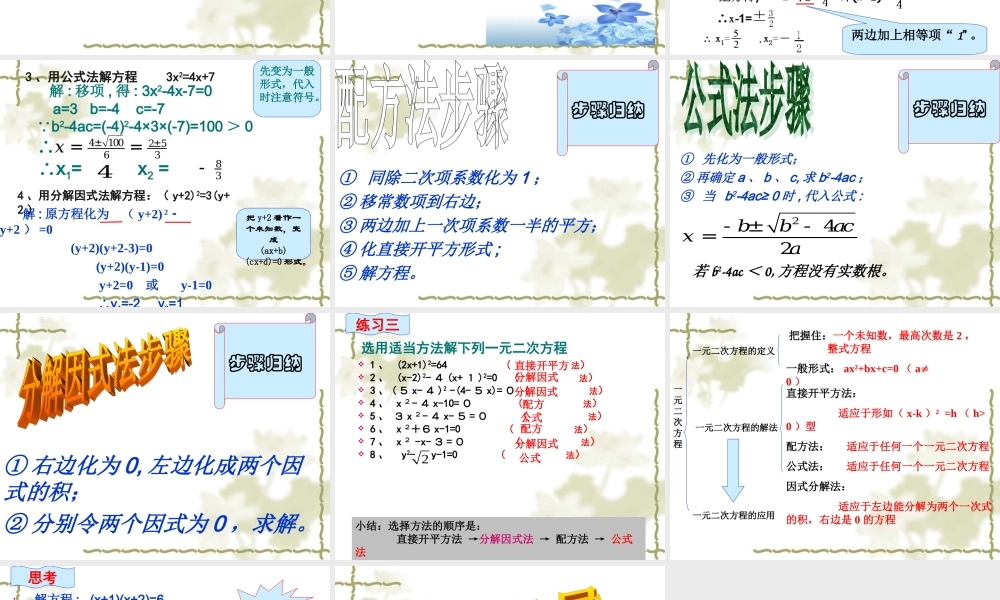
(下一次课)定义及一般形式 : 只含有一个未知数 , 未知数的最高次数是 ______ 的 ___ 式方程 , 叫做一元二次方程。一般形式 :________________二次整ax2+bx+c=o (a≠o)练习一1、判断下面哪些方程是一元二次方程222221x2y24(1)x -3x+4=x -7 ( ) (2) 2X = -4 ( )(3)3 X+5X-1=0 ( ) (4) 3x -20 ( )(5)13 ( )(6)0 ( )xy√ √ × × × × 练习二2、把方程( 1-x)(2-x)=3-x2 化为一般形式是: ___________, 其二次项系数是____, 一次项系数是 ____, 常数项是____.3、方程( m-2)x|m| +3mx-4=0 是关于 x的一元二次方程,则 ( )A.m=±2 B.m=2 C.m=-2 D.m≠ ±2 2x2-3x-1=02-3-1C解一元二次方程的方法有几种 ? 例 : 解下列方程 1、用直接开平方法: (x+2)2= 9 2 、用配方法解方程 4x2-8x-5=0解 : 两边开平方 , 得 : x+2= ±3 ∴ x=-2±3 ∴ x1=1, x2=-5右边开平方后,根号前取“ ±” 。两边加上相等项“ 1” 。 解 : 移项 , 得 : 3x2-4x-7=0 a=3 b=-4 c=-7 b∵2-4ac=(-4)2-4×3×(-7)=100 > 0 ∴ x∴1= x2 = 解 : 原方程化为 ( y+2) 2﹣ 3 ( y+2 ) =0 (y+2)(y+2-3)=0 (y+2)(y-1)=0 y+2=0 或 y-1=0 ∴y1=-2 y2=141002 563x±±==先变为一般形式,代入时注意符号。83-把 y+2 看作一个未知数,变成(ax+b)(cx+d)=0 形式。3 、用公式法解方程 3x2=4x+74 、用分解因式法解方程:( y+2)2=3(y+2 )4① 同除二次项系数化为 1 ;② 移常数项到右边;③ 两边加上一次项系数一半的平方;④ 化直接开平方形式 ;⑤ 解方程。步骤归纳① 先化为一般形式;② 再确定 a 、 b 、 c, 求 b2-4ac ;③ 当 b2-4ac≥ 0 时 , 代入公式 :2±42bbacxa--=步骤归纳若 b2-4ac < 0, 方程没有实数根。① 右边化为 0, 左边化成两个因式的积;② 分别令两个因式为 0 ,求解。步骤归纳选用适当方法解下列一元二次方程 1 、 (2x+1)2=64 ( 法) 2 、 (x-2)2- 4 (x+ 1 )2=0 ( 法) 3 、 ( 5 x- 4 )2 -(4- 5 x)= 0 ( 法) 4 、 x 2- 4 x-10= 0 ( 法) 5 、 3 x 2- 4 x- 5 = 0 ( 法) 6 、 x 2+6 x-1=0 ( 法) 7 、 x 2 -x- 3 = 0 ( 法) 8 、 y2- y-1=0 ( 法) 2小结:选择方法的顺序是: 直接开平方法 →分解因式法 → 配方法 → 公式法分解因式分解因式 配方公式配方分解因式公式直接开平方练习三一元二次方程一元二次方程的定义一元二次方程的解法一元二次方程的应用把握住:一个未知数,最高次数是 2 , 整式方程一般形式: ax²+bx+c=0 ( a0 )直接开平方法: 适应于形如( x-k )² =h ( h>0 )型 配方法: 适应于任何一个一元二次方程公式法: 适应于任何一个一元二次方程因式分解法: 适应于左边能分解为两个一次式的积,右边是 0 的方程1.解方程 : (x+1)(x+2)=62. 已知 : (a2+b2)(a2+b2-3)=10 求 a2+b2 的值。中考直击思考