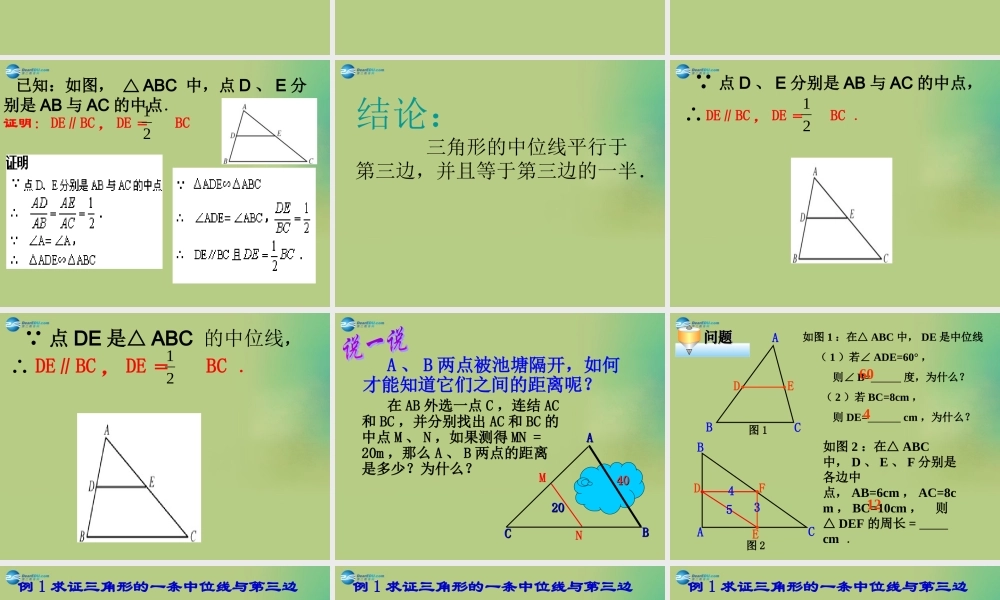
CBAFED 连接三角形两边中点的线段,叫做 三角形的中位线.AF 是△ ABC 的中线;DE 是△ ABC 的中位线.CBAFED 理解三角形的中位线定义的两层含义:② 如果 DE 为△ ABC 的中位线,那么 D 、 E 分别为 AB 、 AC 的 .① 如果 D 、 E 分别为 AB 、 AC 的中点, 那么 DE 为△ ABC 的 ;CBAED中位线中点三角形的中位线有哪些性质呢?1 、画△ ABC ;2 、画△ ABC 的中线 DE ;3 、量出 DE 和 BC 的长度,量出∠ ADE 和∠ B 的度数;4 、猜想 DE 和 BC 之间有什么关系.为什么? 猜想:猜想: DE∥BC , DE = BC .21 已知:如图, △ ABC 中,点 D 、 E 分别是 AB 与 AC 的中点.证明: DE∥BC , DE = BC21.结论: 三角形的中位线平行于第三边,并且等于第三边的一半. ∵ 点 D 、 E 分别是 AB 与 AC 的中点,∴ DE∥BC , DE = BC .21 ∵ 点 DE 是△ ABC 的中位线,∴ DE∥BC , DE = BC .21 A 、 B 两点被池塘隔开,如何才能知道它们之间的距离呢?MN 在 AB 外选一点 C ,连结 AC和 BC ,并分别找出 AC 和 BC 的中点 M 、 N ,如果测得 MN = 20m ,那么 A 、 B 两点的距离是多少?为什么?CCBBAA20204040如图 1 :在△ ABC 中, DE 是中位线 ( 1 )若∠ ADE=60° , 则∠ B= 度,为什么? ( 2 )若 BC=8cm , 则 DE= cm ,为什么? 如图 2 :在△ ABC中, D 、 E 、 F 分别是各边中点, AB=6cm , AC=8cm , BC=10cm , 则△ DEF 的周长 = cm .图 1图 260412ABCD EBACD EF543问题问题例 1 求证三角形的一条中位线与第三边上的中线互相平分.例 1 求证三角形的一条中位线与第三边上的中线互相平分.已知:如图所示,在△ ABC 中, AD = DB ,BE = EC , AF = FC .求证: AE 、 DF 互相平分.FEDBA例 1 求证三角形的一条中位线与第三边上的中线互相平分. 证明 连结 DE 、 EF .∵ AD = DB , BE = EC ,∴ DE∥AC (三角形的中位线平行于第三边并且等于第三边的一半).同理 EF∥AB .∴ 四边形 ADEF 是平行四边形.∴ AE 、 DF 互相平分(平行四边形的对角线互相平分). 例 2 如图,△ ABC 中, D 、 E 分别是边 BC 、 AB 的中点, AD 、 CE 相交于G .求证: 31ADGDCEGEDECBA例 2 如图,△ ABC 中, D 、 E 分别是边 BC 、 AB 的中点, AD 、 CE 相交于G .求证: 31 ADGDCEGE 证明 :连结 ED , ∵ D 、 E 分别是边 BC 、 AB 的中点,∴ DE∥AC ,21ACDE(三角形的中位线平行于第三边并且等于第三边的一半)∴ △ ACG∽△DEG ,∴ 21ACDEAGGDGCGE∴ 31 ADGDCEGE