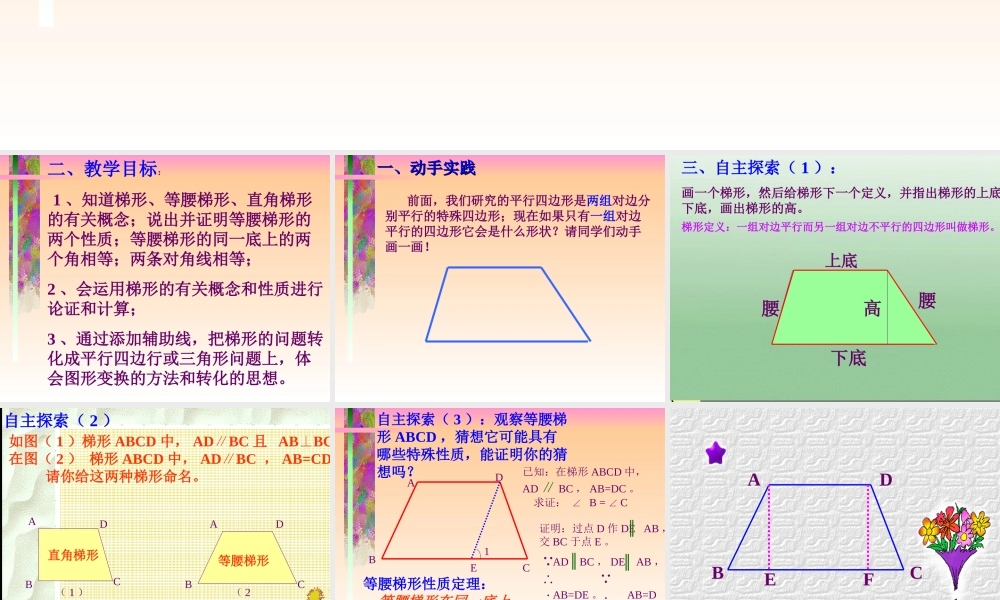
梯 形梯 形 二、教学目标: 1 、知道梯形、等腰梯形、直角梯形的有关概念;说出并证明等腰梯形的两个性质;等腰梯形的同一底上的两个角相等;两条对角线相等;2 、会运用梯形的有关概念和性质进行论证和计算;3 、通过添加辅助线,把梯形的问题转化成平行四边行或三角形问题上,体会图形变换的方法和转化的思想。 一、动手实践一、动手实践 前面,我们研究的平行四边形是两组对边分别平行的特殊四边形;现在如果只有一组对边平行的四边形它会是什么形状?请同学们动手画一画! 上底下底腰腰高三、自主探索( 1 ):画一个梯形,然后给梯形下一个定义,并指出梯形的上底、下底,画出梯形的高。 梯形定义:一组对边平行而另一组对边不平行的四边形叫做梯形。 如图( 1 )梯形 ABCD 中, ADBC∥且 ABBC.⊥在图( 2 ) 梯形 ABCD 中, ADBC ∥, AB=CD 。 请你给这两种梯形命名。等腰梯形直角梯形ABCDABCD自主探索( 2 )( 1 )( 2) ABCDE自主探索( 3 ):观察等腰梯形 ABCD ,猜想它可能具有哪些特殊性质,能证明你的猜想吗?1证明:过点 D 作 DE AB ,交 BC 于点 E 。 AD BC , DE AB , AB=DE 。 AB=DC , DE=DC 。 ∠ 1= ∠ C 。 ∠ 1= ∠ B , ∠ B= ∠ C 。∥∥ ∥ ∴∴∴∴等腰梯形性质定理: 等腰梯形在同一底上的两个角相等。已知:在梯形 ABCD 中,AD ∥ BC , AB=DC 。 求证: ∠ B = ∠ C ABDCEF ACDBE自主探索四:等腰梯形是轴对称图形吗? 如何证明呢? 例 1 :等腰梯形的对角线相等已知:梯形 ABCD 中, ADBC∥, AB=DC.求证: AC=BD.证明:在梯形 ABCD 中, AB = DC ,∴∠ABC =∠ DCB ,又 BC = CB ,∴△ABCDCB.≌△ ∴AC = BC.ABCD ABCDEF例 2 (补充)如图 , 已知梯形 ABCD 中, DC∥AB ,∠ A=40° ,∠ B=70° .求证: AB=AD+CD .12证明:过点 D 作 DE BC ∥交 AB 于点E 。 DE CB DC BC ∥∥∴ DC=EB ,∠ 1= B ∠。 ∠ A= 40° , ∠ B= 70°∴ ∠ 1= 2= 70° ∠∴ AD=AE 。 AB=AE+EB 。 ∴ AB=AD+CD . 反馈练习:1 、判断题: ( 1 )一组对边平行的四边形是梯形 ( ) ( 2 )一组对边平行且不相等的四边形是梯形 ( ) ( 3 )等腰梯形的两个底角相等 . ( ) ( 4 )等腰梯形的对角线相等 . (...