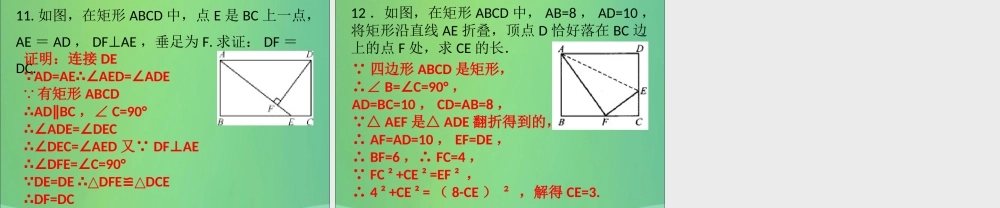
巩固提高精典范例(变式练习)第 4 课时 矩形的性质与判定( 1 )第一章 特殊的平行四边形【例 1 】已知四边形 ABCD ,若AB CD∥, AD BC∥,且∠ A = 90° ,则四边形ABCD 为 ___________ .精 典 范 例矩形1. 矩形的一条边长为 3cm ,对角线为 5cm ,则矩形的周长为 ,其面积为 . 变 式 练 习14cm12cm【例 2 】已知矩形 ABCD 中,矩形 ABCD 的面积为 24 cm ² ,若 BC=6 cm ,则 AB 的长是 , AC 的长是 ________ cm , BD的长为 ________ cm精 典 范 例42. 如图,在矩形 ABCD 中,对角线 AC , BD 相交于点 O ,若 OA = 2 ,则 BD 的长为 ( )A.4 B.3 C.2 D.1变 式 练 习A【例 3 】如图,在 Rt ABC△中,∠ ACB = 90° ,AB = 10 cm , D 为 AB 的中点,则 CD = ____________cm.精 典 范 例53. 在直角三角形,已知两边长分别是 12 和 5 ,则任斜边上的中线长为( )A.26 B.13 C.6.5 D.6.5 或 6精 典 范 例D巩 固 提 高4 .下列命题是假命题的是 ( ) A .矩形的对角线相等 B .矩形的对边相等 C .矩形的对角线互相平分 D .矩形的对角线互相垂直D巩 固 提 高5. 如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠ 1 +∠ 2 的度数是 ( )A . 30° B . 60° C . 90° D . 120°C巩 固 提 高6. 如图,在矩形 ABCD 中,对角线 AC , BD 交于点 O ,下列说法错误的是( )A . AB∥ DCB . AC=BDC . AC⊥BDD . OA=OCC巩 固 提 高7. 矩形 ABCD 的两条对角线相交于点O ,∠ AOB=60° , AB=2 ,则 BC 的长是( )A . 2 B . 4 C . 2 D . 48. 矩形的两条邻边分别是 , 2 ,则它的一条对角线的长是 ______ .C3巩 固 提 高9. 如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O ,且 AB = OA = 2 cm ,则 AD 的长为 ____________ . 2巩 固 提 高10. 如图,一根长 a m 的木棍 (AB) ,斜靠在与地面 (OM) 垂直的墙 (ON) 上,设木棍的中点为P ,若木棍 A 端沿墙下滑,且 B 端沿地面向右滑行.请判断木棍滑动的过程中,点 P 到点 O的距离 _________( 填“发生”或“不发生” )变化.不发生巩 固 提 高11. 如图,在矩形 ABCD 中,点 E 是 BC 上一点,AE = AD , DFAE⊥,垂足为 F. 求证: DF =DC.证明:连接 DEAD=AEAED=ADE∵∴∠∠∵ 有矩形 ABCDAD BC∴∥,∠ C=90° ADE=DEC ∴∠∠DEC=AED∴∠∠又∵ DFAE⊥DFE=C=90°∴∠∠DE=DE DFEDCE∵∴△≌△DF=DC∴巩 固 提 高12 .如图,在矩形 ABCD 中, AB=8 , AD=10 ,将矩形沿直线 AE 折叠,顶点 D 恰好落在 BC 边上的点 F 处,求 CE 的长.∵ 四边形 ABCD 是矩形,∴∠ B=C=90°∠,AD=BC=10 , CD=AB=8 ,∵△ AEF 是△ ADE 翻折得到的,∴ AF=AD=10 , EF=DE ,∴ BF=6 ,∴ FC=4 ,∵ FC ² +CE ² =EF ² ,∴ 4 ² +CE ² = ( 8-CE ) ² ,解得 CE=3.