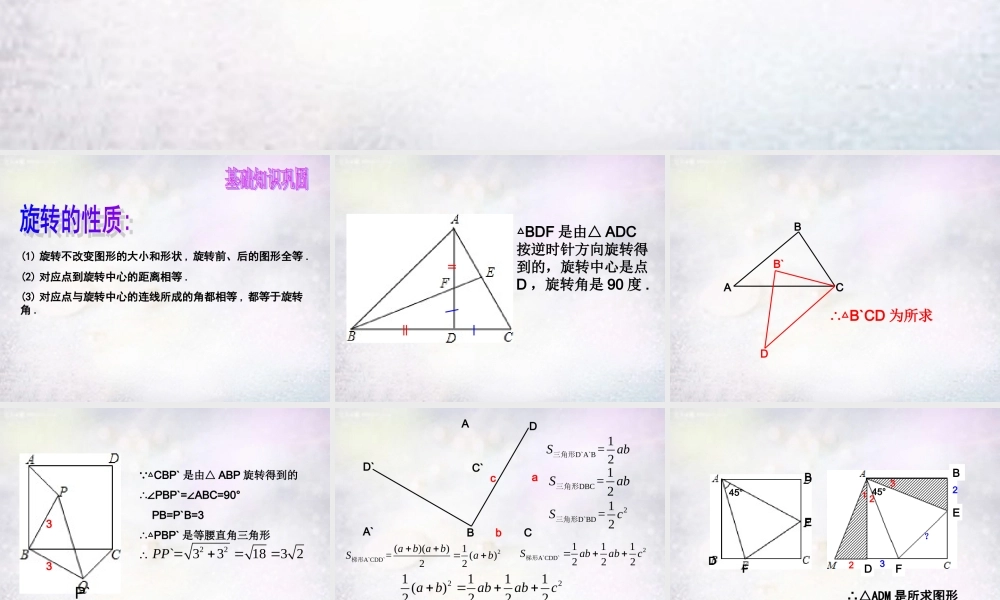
(2) 对应点到旋转中心的距离相等 .(1) 旋转不改变图形的大小和形状 , 旋转前、后的图形全等 .(3) 对应点与旋转中心的连线所成的角都相等 , 都等于旋转角 .△BDF 是由△ ADC按逆时针方向旋转得到的,旋转中心是点D ,旋转角是 90 度 .BACB`D∴△B`CD 为所求33∵△CBP` 是由△ ABP 旋转得到的∴∠PBP`= ABC=90°∠ PB=P`B=3∴△PBP` 是等腰直角三角形∴22`33183 2PP P`D`C`A`BCADabcD`A`B1= 2Sab三角形DBC1= 2Sab三角形2D`BD1= 2Sc三角形2A`CDD`()()1=()22ab abSab梯形2A`CDD`111222Sababc梯形221111()2222abababc222bc化简得:aBEFD45°45°DBFE∴△ADM 是所求图形23?2213BEFD45°∴△ADM 是所求图形23?2∵△ADM 是△ ABE 绕点 A 顺时针旋转 90 度得到的∴DM=BE=2 , AE = AM ∠MAE=90 °∵ ∠EAF=45°∴∠MAF=45°= FAE∠∵AF=AF∴△AEFAMF≌△∴EF=MF=MD+DF=2+3=5F123如图, 在矩形 ABCD 中, AD=2AB , E 是 AD 的中点,一个三角尺的直角顶点与点 E 重合,将三角板绕点 E 按顺时针方向旋转,当三角板的两直角边与 AB , BC 分别相交于点 M , N时,观察并测量 EM 与 EN 的长度,你有什么发现?说明你的理由 .ABCD1234ABDE△ACE 绕点 C 逆时针旋转 60 度得到△ BCD△ANC 绕点 C 逆时针旋转 60 度得到△ BCM△MCD 绕点 C 顺时针旋转 60 度得到△ NCEMN1 2E把△ ADQ 绕点 A 顺时针旋转 90 度得到△ ABE∴∠E= AQD∠, BE=DQ , ∠EAQ=90°∴∠EAP+∠ 1=90°∵ ∠AQD+∠ 2=90° ∠1=∠ 2∴∠AQD= EAP∠∵ ∠E =∠ AQD∴∠E= EAP∠∴PA=PE∵ PE=PB+EB∴PA=PB+DQ