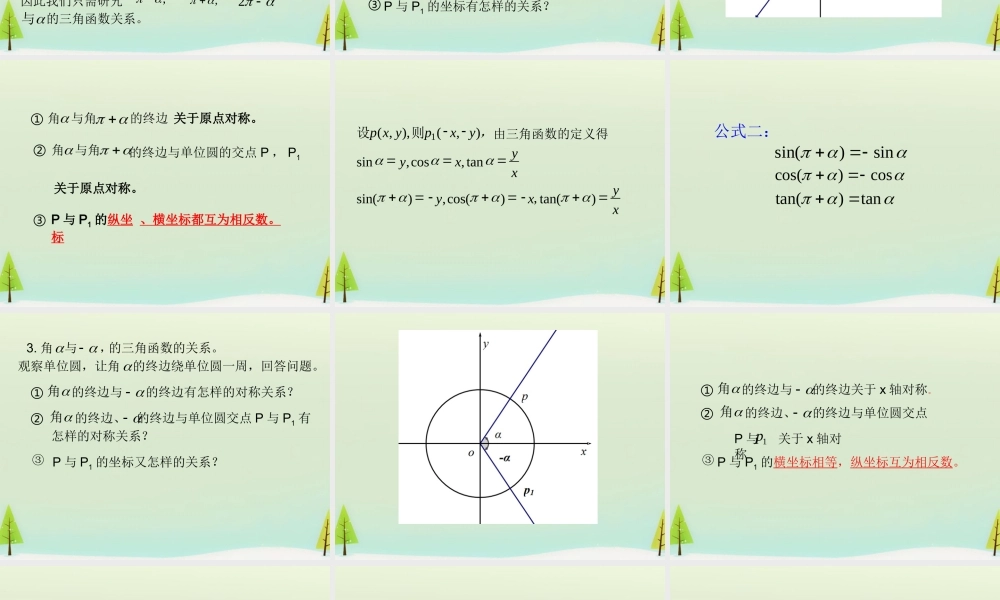
1.3 三角函数的诱导公式 一、复习引入1 、正弦函数,余弦函数的定义 :2 、终边相同的角的三角函数值有什么关系?设角 α 的终边与单位圆交于点 P(x,y)xyxytan,cos,sin则公式一:)(zk tan)2tan(cos)2cos(sin)2sin(kkk公式一的用途: 公式一把求任意角的三角函数值转化为求)2,0[ 范围的角的三角函数值问题。我们对)2,0[ 范围内角的三角函数值很熟悉。若把内角的三角函数值转化为 的三角函数值,那么任意角的三角函数值就可以求出,这就是我们这节课要解决的问题。)2,0[)2,0[二、探究新知1. 对于任何一个)2,0[内的角有四种可能:,其中)2,0[ )2,0[,当),2[,当)23,[,当)2,23[,2当与因此我们只需研究, , 2的三角函数关系。观察单位圆,回答下列问题:① 角 与角的终边有怎样的对称关系?② 角 与角的终边与单位圆的交点 P , P1之间有怎样的对称关系?③ P 与 P1 的坐标有怎样的关系?2. 角 α与 的三角函数的关系。① 角 与角的终边② 角 与角的终边与单位圆的交点 P , P1③关于原点对称。关于原点对称。P 与 P1 的纵坐标、横坐标都互为相反数。xyxyxyxy,yxpyxp)tan(,)cos(,)sin(tan,cos,sin),(),,(1则设由三角函数的定义得公式二:cos)cos(sin)sin(tan)tan(3. 角与 的三角函数的关系。,观察单位圆,让角 的终边绕单位圆一周,回答问题。①角的终边与的终边有怎样的对称关系?②角的终边、 的终边与单位圆交点 P 与 P1 有怎样的对称关系?③ P 与 P1 的坐标又怎样的关系?P 与 P1 的横坐标相等,纵坐标互为相反数。①角的终边与的终边关于 x 轴对称。②角的终边、 的终边与单位圆交点③P 与 关于 x 轴对称1pcos)cos(sin)sin(tan)tan(公式三tan)tan()2tan(cos)cos()2cos(sin)sin()2sin(2kkk,,k即相等故其同名三角函数值也的终边相同与因为角设角 的终边与单位圆交于点 P , 的终边与单位圆交于 P1 ,当 为任意角时:角 的终边与 ...