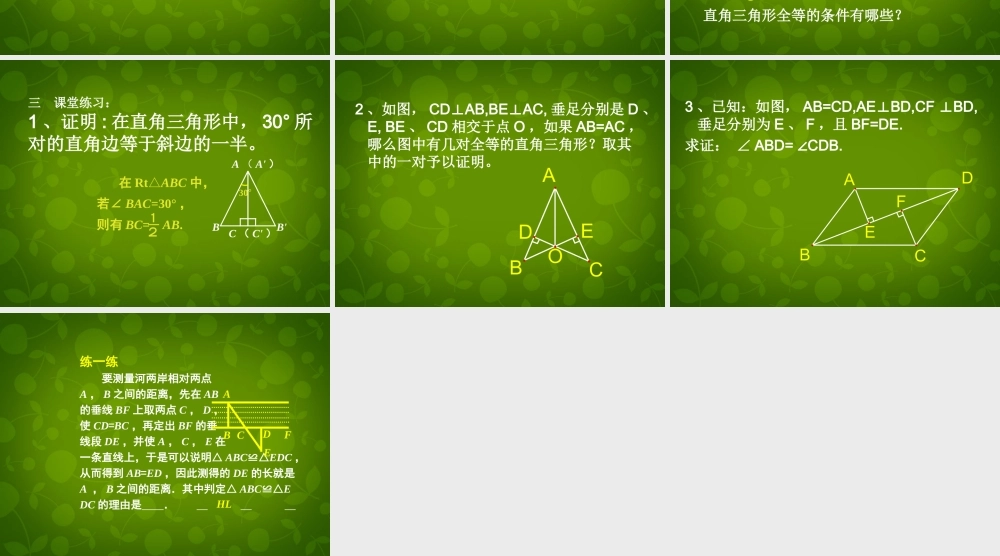
直角三角形全等的判定(一) 已知:如图,在△ ABC 中, AD⊥BC , AB=AC . 求证:△ ABD≌△ACD . 一般地,斜边和一条直角边对应相等的两个直角三角形全等. 猜想:ABCDA ( A' )C ( C' )CAB 已知:如图,在△ ABC 和△ A'B'C' 中,∠ ACB=∠A'C'B'=90° , AB=A'B' , AC=A'C' . 求证:△ ABC≌△A'B'C' .ACB'A'C'BBB 此时拼合所成的图形是一个三角形吗? 证明:把△ ABC 和△A'B'C' 拼合在一起,使 AC 与A'C' 重合,且点 B , B' 落在 AC 两侧 . ∵∠ACB=∠A'C'B'=90° , ∴∠BCB'=180° ,即 B , C , B' 在同一条直线上.B'BA ( A' )C ( C' ) 在△ ABC 和△ AB'C 中, ∠B=∠B' (已证), ∠ACB=∠ACB' (已知), AB=AB' (已知), ∴ △ABC≌△AB'C ( AAS ). 即 △ ABC≌△A'B'C' . ∵ AB=AB' , ∴∠B=∠B' (等边对等角).B'BA ( A' )C ( C' ) 斜边和一条直角边对应相等的两个直角三角形全等. 定理(简写为“ HL” )已知:如图,在△ ABC 和 △ A,B,C, 中,∠ ACB= A∠,C,B,=90o , BC=B,C, , AC=A,C,.△ ABC 和△ A,B,C, 全等吗?为什么?A'C'B'ACB直角三角形全等的条件有哪些? B'BA ( A' )C ( C' )30° 在 Rt△ABC 中,若∠ BAC=30° ,则有 BC= AB.12三 课堂练习:1 、证明 : 在直角三角形中, 30° 所对的直角边等于斜边的一半。2 、如图, CDAB,BEAC,⊥⊥垂足分别是 D 、E, BE 、 CD 相交于点 O ,如果 AB=AC ,哪么图中有几对全等的直角三角形?取其中的一对予以证明。OABCDE3 、已知:如图, AB=CD,AEBD,CF BD,⊥⊥垂足分别为 E 、 F ,且 BF=DE.求证: ∠ ABD= CDB.∠ABCDFE 要测量河两岸相对两点A , B 之间的距离,先在 AB的垂线 BF 上取两点 C , D ,使 CD=BC ,再定出 BF 的垂线段 DE ,并使 A , C , E 在一条直线上,于是可以说明△ ABC≌△EDC ,从而得到 AB=ED ,因此测得的 DE 的长就是A , B 之间的距离.其中判定△ ABC≌△EDC 的理由是 . 练一练AB CDEF HL