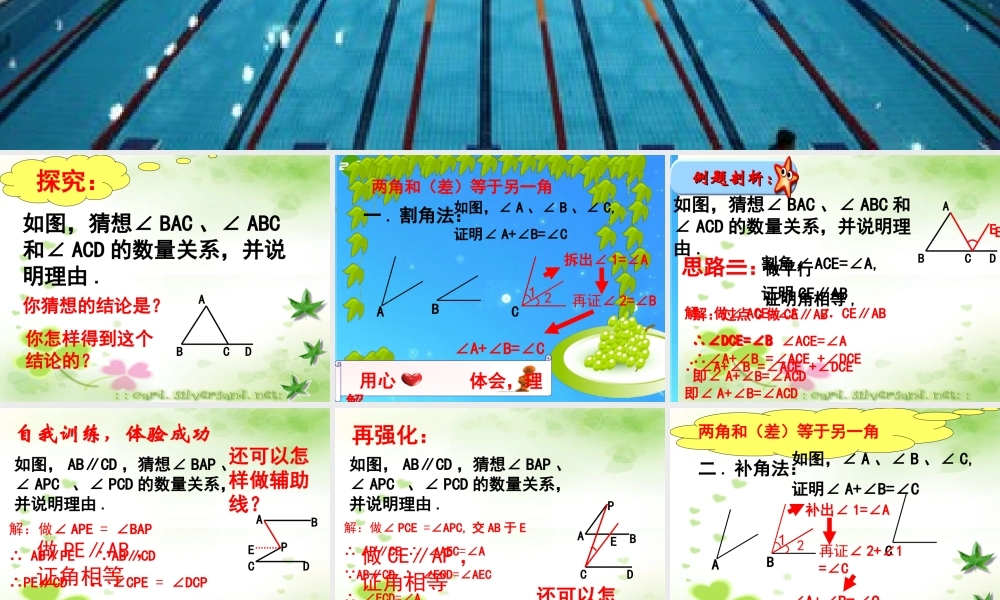
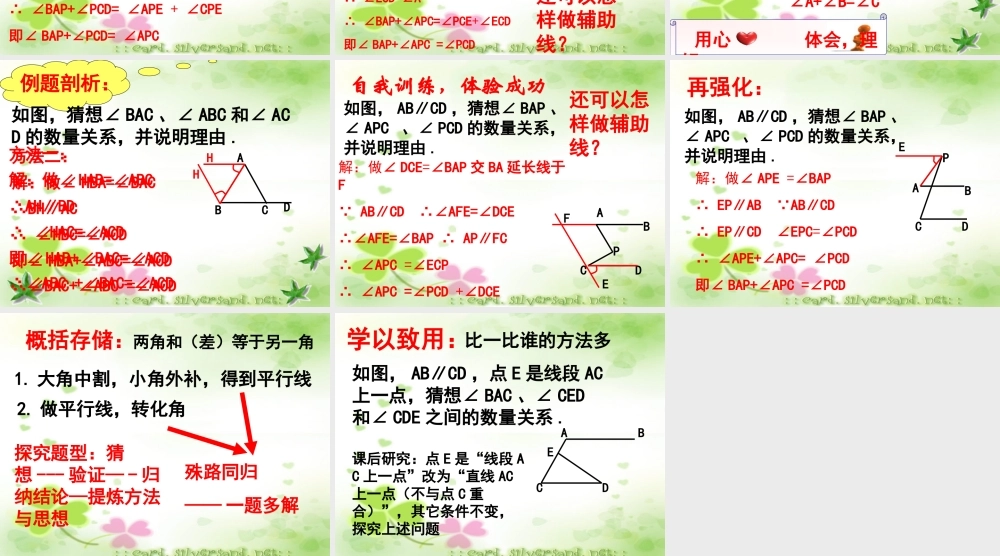
平行线专题课 如图,猜想∠ BAC 、∠ ABC和∠ ACD 的数量关系,并说明理由 .ABCD探究:你猜想的结论是?你怎样得到这个结论的? 用心 体会,理解两角和(差)等于另一角一 . 割角法:如图,∠ A 、∠ B 、∠ C,证明∠ A+∠B=∠CABC1拆出∠ 1=∠A2再证∠ 2=∠B∠A+∠B=∠C 例题剖析:例题剖析:ABCD如图,猜想∠ BAC 、∠ ABC 和∠ ACD 的数量关系,并说明理由 .思路一:割角∠ ACE=∠A,证明 CE∥AB解:做∠ ACE=∠A ∴ CE∥AB ∴∠DCE=∠B ∴∠A+∠B =∠ACE +∠DCE即∠ A+∠B=∠ACDE思路二:做平行 证明角相等 ,E解:过点 C 做 CE∥AB ∴∠DCE=∠B ∠ACE=∠A∴∠A+∠B =∠ACE +∠DCE即∠ A+∠B=∠ACD 自我训练,体验成功如图, AB∥CD ,猜想∠ BAP 、∠ APC 、∠ PCD 的数量关系,并说明理由 .ABPCDE解:做∠ APE = ∠BAP∴ AB∥PE AB∥CD∴PE∥CD ∴ ∠CPE = ∠DCP∴ ∠BAP+∠PCD= ∠APE + ∠CPE 即∠ BAP+∠PCD= ∠APC还可以怎样做辅助线?做 PE∥AB ,证角相等 再强化:如图, AB∥CD ,猜想∠ BAP 、∠ APC 、∠ PCD 的数量关系,并说明理由 .ABCDPE解:做∠ PCE =∠APC, 交 AB 于 E∴ AP∥CE ∴ ∠AEC=∠A AB∥CD ∴ ∠ECD=∠AEC∴ ∠ECD=∠A∴ ∠BAP+∠APC=∠PCE+∠ECD即∠ BAP+∠APC =∠PCD做 CE∥AP ,证角相等还可以怎样做辅助线? 两角和(差)等于另一角二 . 补角法:ABC1补出∠ 1=∠A2再证∠ 2+∠1=∠C∠A+∠B=∠C 用心 体会,理解如图,∠ A 、∠ B 、∠ C,证明∠ A+∠B=∠C 如图,猜想∠ BAC 、∠ ABC 和∠ ACD 的数量关系,并说明理由 .ABCD例题剖析:H方法一:解:做∠ HAB=∠ABC ∴AH∥BD∴ ∠HAC=∠ACD 即∠ HAB+∠BAC=∠ACD ∴∠ABC +∠BAC=∠ACD 方法二:解:做∠ HBA=∠BAC ∴BH∥AC∴ ∠HBC=∠ACD 即∠ HBA+∠ABC=∠ACD ∴∠BAC+∠ABC =∠ACD H 自我训练,体验成功如图, AB∥CD ,猜想∠ BAP 、∠ APC 、∠ PCD 的数量关系,并说明理由 .ABPCDE解:做∠ DCE=∠BAP 交 BA 延长线于F AB∥CD ∴∠AFE=∠DCE∴∠AFE=∠BAP ∴ AP∥FC ∴ ∠APC =∠ECP∴ ∠APC =∠PCD +∠DCE 即∠ BAP+∠PCD=∠APC还可以怎样做辅助线?F 再强化:如图, AB∥CD ,猜想∠ BAP 、∠ APC 、∠ PCD 的数量关系,并说明理由 .ABCDPE解:做∠ APE =∠BAP∴...