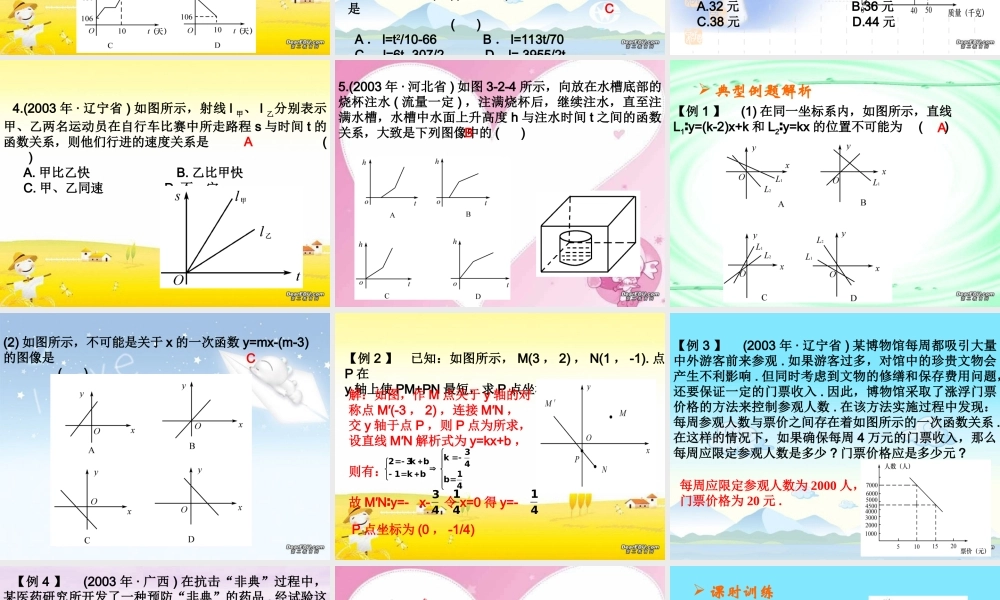
第三章第二课时:一次函数的图象及其性质 要点、考点聚焦 课前热身 典型例题解析 课时训练 要点、考点聚焦1 、一次函数的定义:一般地,如果 y=kx+b(k,b 是常数,k≠0) ,那么 y 叫做 x 的一次函数 . 当 b=0 时,一次函数 y=kx+b 成为 y=kx(k 是常数, k≠0) ,这时 y 叫做 x 的正比例函数 ( 或者说 y 与 x 成正比例 ). 2 、一次函数的图像是直线,其性质是: (1) 当 k > 0 时, y 随 x 的增大而增大 . (2) 当 k < 0 时, y 随 x 的增大而减小 . 3 、 y=kx+b 经过的象限情况:(1)k > 0 , b > 0 时,图像过第一、二、三象限;(2)k > 0 , b < 0 时,图像过第一、三、四象限;(3)k < 0 , b > 0 时,图像过第一、二、四象限;(4)k < 0 , b < 0 时,图像过第二、三、四象限 .4 、画正比例函数的图像,一般取 (0 , 0) , (1 , k)两点,画一次函数的图像,一般取直线与坐标轴的两交点 . 要点、考点聚焦1. (2003 年 · 北京市 ) 如图 3-2-1 所示,三峡工程在 6 月1 日至 6 月 10 日下阐蓄水期间,水库水位由 106 米升至 135 米,高峡平湖初现人间 . 假设水库水位匀速上升,那么下列图像中,能正确反映这 10 天水位 h( 米 ) 随时间 t( 天 ) 变化的是 ( ) 课前热身B请你根据上述数据分析判断,水银柱的长度 l(mm) 与体温计的读数 t()(35≤t≤42)℃之间存在的函数关系是 ( ) A . l=t2/10-66 B . l=113t/70 C . l=6t- 307/2 D. l= 3955/2t2. (2003 年 · 北京海淀区 ) 某同学在测量体温时意识到体温计的读数与水银柱的长度之间可能存在着某种函数关系,就此他与同学们选择了一种类型的体温计,经历了收集数据、分析数据、得出结论的探索过程,他们收集到的数据如下: C体温计的读数 t()℃3536373839404142水银柱的长度l(mm)56.562.5 68.5 74.5 80.5 86.5 92.5 98.5 3.(2003 年 · 武汉市 ) 如图 3-2-2 所示 . 小李以每千克 0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价 0.4 元,全部售完,销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚了 ( ) BA.32 元 B.36 元C.38 元 D.44 元4.(2003 年 · 辽宁省 ) 如图所示,射线 l 甲、 l 乙分别表示甲、乙两...