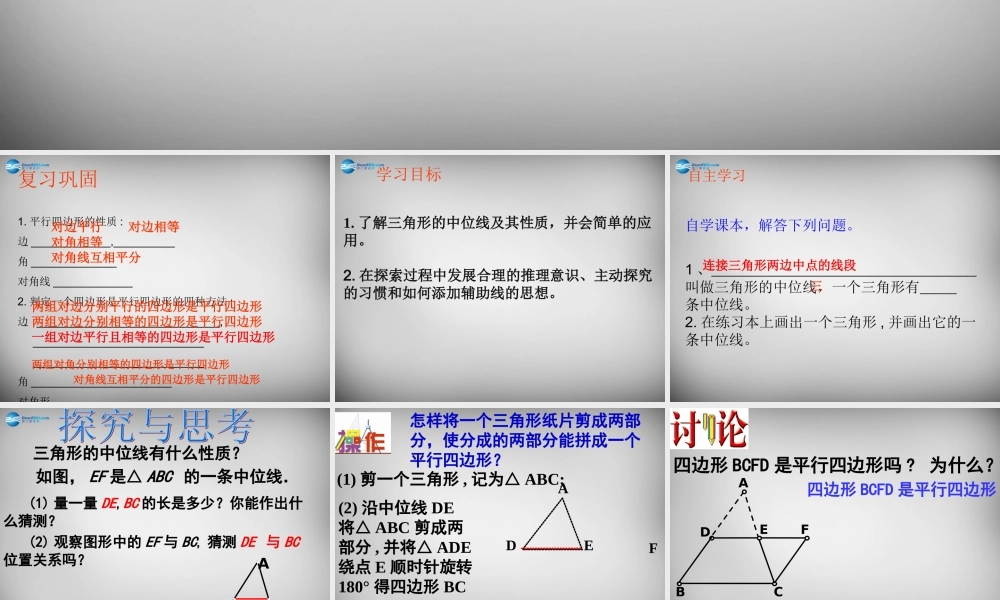
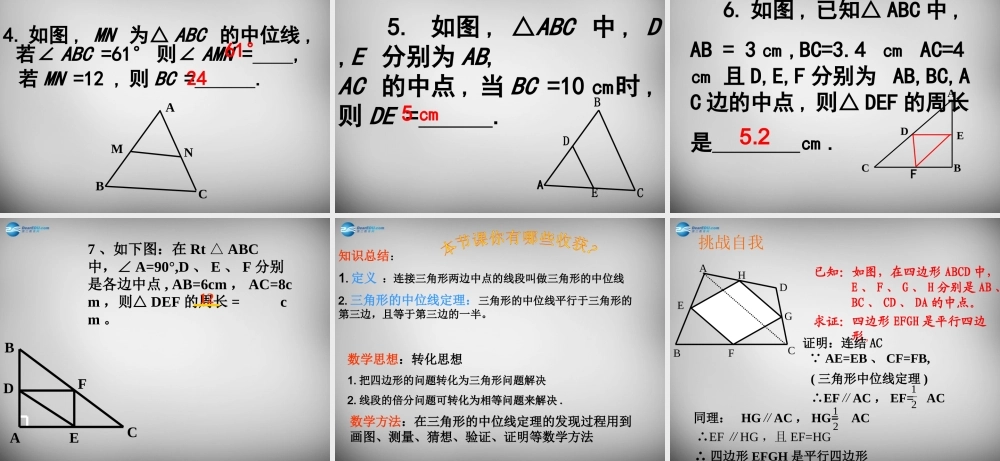
18.1.2 平行四边形的判定( 2 )复习巩固1. 平行四边形的性质 :边 _____________,__________角 ______________对角线 _____________2. 判定一个四边形是平行四边形的四种方法 :边 ______________________________, ____________________________ ____________________________角 _______________________对角形 _____________________对边平行 对边相等对角相等对角线互相平分两组对边分别平行的四边形是平行四边形两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形 对角线互相平分的四边形是平行四边形1. 了解三角形的中位线及其性质,并会简单的应用。2. 在探索过程中发展合理的推理意识、主动探究的习惯和如何添加辅助线的思想。 学习目标自学课本,解答下列问题。1 、 叫做三角形的中位线,一个三角形有 条中位线。2. 在练习本上画出一个三角形 , 并画出它的一条中位线。连接三角形两边中点的线段三自主学习三角形的中位线有什么性质?如图, EF 是△ ABC 的一条中位线. (1) 量一量 DE,BC 的长是多少?你能作出什么猜测? (2) 观察图形中的 EF 与 BC, 猜测 DE 与 BC 位置关系吗?CABD E 怎样将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?(1) 剪一个三角形 , 记为△ ABC;(2) 沿中位线 DE将△ ABC 剪成两部分 , 并将△ ADE绕点 E 顺时针旋转180° 得四边形 BCFD.ABCDEF四边形 BCFD 是平行四边形吗 ? 为什么?四边形 BCFD 是平行四边形DEBCAFABCDEF DE=EF 1=2 AE=EC∠∠∴△ADE CFE≌ △证明:如 图,延 长 DE 到 F ,使 EF=DE ,连 结 CF.∴AD=FC 、∠ A=ECF∠∴ABFC∥又 AD=DB ∴BD CF∥且 BD =CF∴ 四边形 BCFD 是平行四边形还有另外的证法吗?∴DFBC∥, DF = BC又 12DEDF12DEBC即 DEBC∥ 已知:在△ ABC 中, DE 是△ ABC 的中位线 求证: DE BC∥,且 DE= BC 。 1212ABCEDF证明:如图,延长 DE 至 F, 使 EF=DE ,连接 CD 、 AF 、 CF AE=EC ∴DE=EF∴ 四边形 ADCF 是平行四边形∴ AD FC又 D 为 AB 中点,∴DB FC∴ 四边形 BCFD 是平行四边形 ∴DE// BC 且 DE=EF=1/2BCCEDFBA证法三:过点 C 作 AB 的平行线交 DE 的延长线于 F CFAB∥,∴∠A=ECF∠又 AE=EC ,∠ AED=CEF∠ ∴...