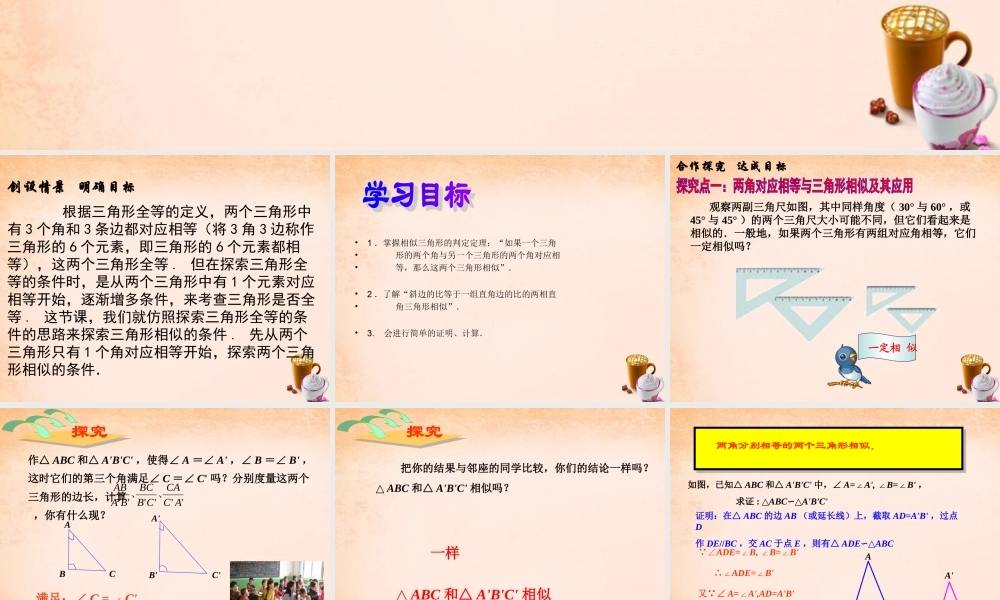
27.2.1 相似三角形的判定第 3 课时 相似三角形的判定( 3 )创设情景 明确目标 根据三角形全等的定义,两个三角形中有 3 个角和 3 条边都对应相等(将 3 角 3 边称作三角形的 6 个元素,即三角形的 6 个元素都相等),这两个三角形全等 . 但在探索三角形全等的条件时,是从两个三角形中有 1 个元素对应相等开始,逐渐增多条件,来考查三角形是否全等 . 这节课,我们就仿照探索三角形全等的条件的思路来探索三角形相似的条件 . 先从两个三角形只有 1 个角对应相等开始,探索两个三角形相似的条件. •1 .掌握相似三角形的判定定理:“如果一个三角• 形的两个角与另一个三角形的两个角对应相• 等,那么这两个三角形相似”. •2 .了解“斜边的比等于一组直角边的比的两相直• 角三角形相似”. •3. 会进行简单的证明、计算. 观察两副三角尺如图,其中同样角度( 30° 与 60° ,或45° 与 45° )的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗? 一定相 似合作探究 达成目标作△ ABC 和△ A'B'C' ,使得∠ A =∠ A' ,∠ B =∠ B' ,这时它们的第三个角满足∠ C =∠ C' 吗?分别度量这两个三角形的边长,计算 ,你有什么现?''''''ACCACBBCBAAB、、探究ABCA'B'C'满足:∠ C = ∠C'''''''ABBCCAA BB CC A△ ABC∽△A'B'C'探究 把你的结果与邻座的同学比较,你们的结论一样吗? △ ABC 和△ A'B'C' 相似吗?一样△ ABC 和△ A'B'C' 相似得到判定两个三角形相似的又一个简便方法:两角分别相等的两个三角形相似.如图,已知△ ABC 和△ A'B'C' 中,∠ A=∠A', ∠B=∠B' , 求证 : △ABC∽△A'B'C'证明:在△ ABC 的边 AB (或延长线)上,截取 AD=A'B' ,过点D作 DE//BC ,交 AC 于点 E ,则有△ ADE∽△ABC ∠ADE=∠B, ∠B=∠B'∴∠ADE=∠B'又 ∠ A=∠A',AD=A'B'∴△ ADE△A'B'C'∴△ A'B'C'∽△ABCABCDEA'B'C'【针对练一】1 .如图,△ ABC 内接于⊙ O ,∠ BAC 的平分线交⊙ O 于点 D ,交 BC 于点 E ,连接 BD .( 1 )请你找出图中所有的相似三角形;( 2 )请选择其中的一对相似三角形予以证明. 解:( 1 )△ DBEDAB∽△;△ DBECAE∽△;△ ABDAEC∽△.( 2 )选择△ ABDAEC∽△. DA 是∠ BAC 的平分线,...