人教版高二数学平行与垂直 课件VIP免费

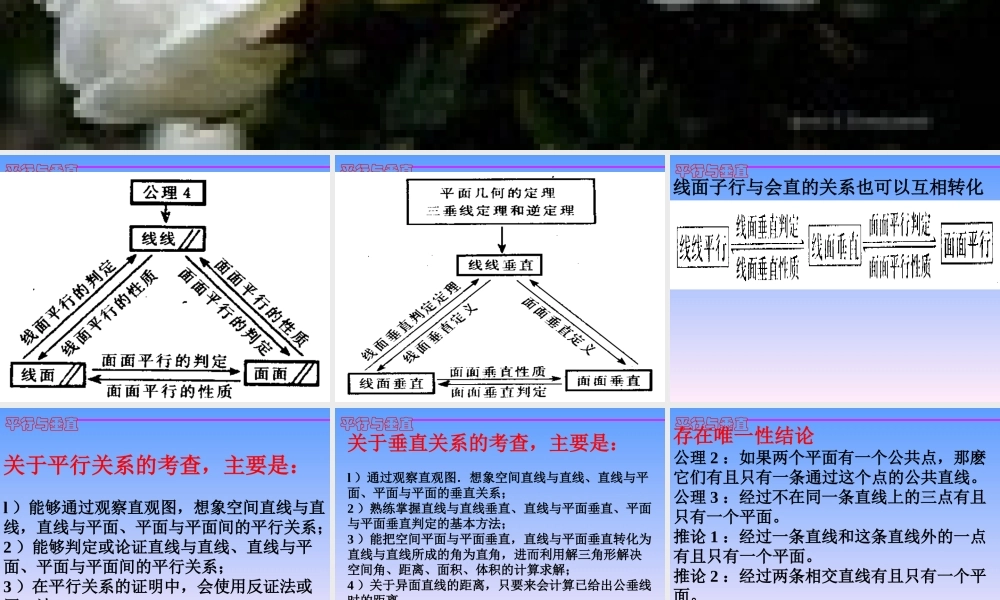
平行与垂直 平行与垂直 平行与垂直 平行与垂直线面子行与会直的关系也可以互相转化 平行与垂直关于平行关系的考查，主要是：l ）能够通过观察直观图，想象空间直线与直线，直线与平面、平面与平面间的平行关系；2 ）能够判定或论证直线与直线、直线与平面、平面与平面间的平行关系；3 ）在平行关系的证明中，会使用反证法或同一法 平行与垂直关于垂直关系的考查，主要是：l ）通过观察直观图．想象空间直线与直线、直线与平面、平面与平面的垂直关系；2 ）熟练掌握直线与直线垂直、直线与平面垂直、平面与平面垂直判定的基本方法；3 ）能把空间平面与平面垂直，直线与平面垂直转化为直线与直线所成的角为直角，进而利用解三角形解决空间角、距离、面积、体积的计算求解；4 ）关于异面直线的距离，只要来会计算已给出公垂线时的距离． 平行与垂直存在唯一性结论公理 2 ：如果两个平面有一个公共点，那麽它们有且只有一条通过这个点的公共直线。公理 3 ：经过不在同一条直线上的三点有且只有一个平面。推论 1 ：经过一条直线和这条直线外的一点有且只有一个平面。推论 2 ：经过两条相交直线有且只有一个平面。推论 3 ：经过两条平行直线有且只有一个平面。 平行与垂直线面垂直的两个性质经过一点有且只有一条直线和一个平面垂直。经过一点有且只有一个平面和一条直线垂直条直线。面面平行的性质过平面外一点有且只有一个平面和已知平面平行。 平行与垂直两直线平行的判定1. 定义：在同一平面内没有公共点的两条直线。2. 公理 4 ： ab∥ ， bc ∥acb∥a3. 直线和平面平行性质定理：a∥ ， a ，∩ =b ab∥4. 直线和平面垂直的性质定理： a ， b ab∥5. 两个平面平行的性质定理：∥ ，∩ =a ，∩ =b ab∥6. a 、 b 、 c ， ac ， bc ab∥ 平行与垂直两直线垂直判定1. 定义：所成角是直角。2. 如果一条直线和两条平行线中的一条垂直，那麽它也和另一条垂直。 即 ab∥ ， ca cb3. 线面垂直定义。即 a ， b ba4. 三垂线定理。即 PA ， AOa ， a    aPO5. 三垂线定理逆定理。即 PA ， aPO ， a AOa6. 三个两两垂直的平面的三条交线两两垂直。（半个定理） 、、两两垂直三条交线 a 、 b 、 c 两两垂直 平行与垂直直线和平面平行的判定1. ...