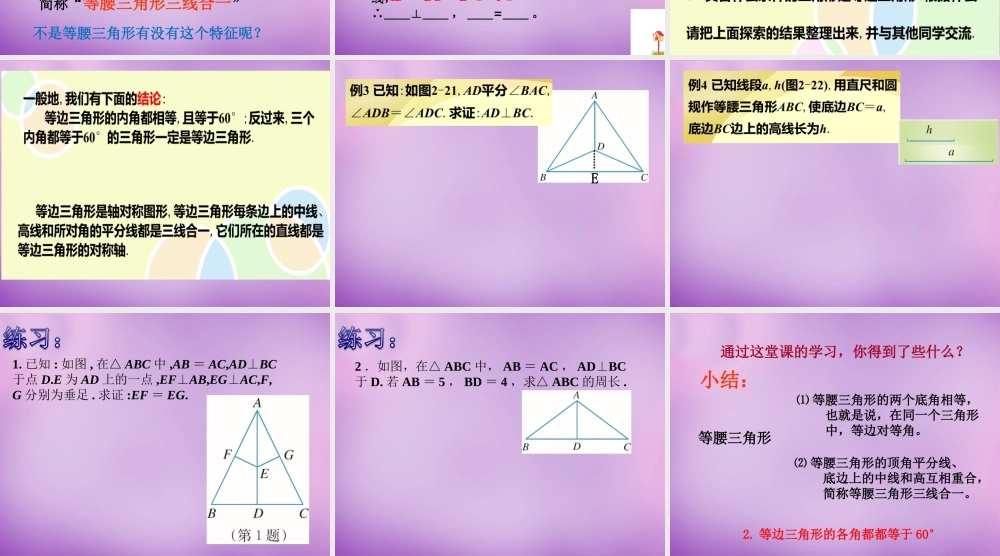
1 、等腰三角形的定义。ABCD2 、等腰三角形是一种特殊的三角形,它除具 有一般三角形的性质外,还有一些特殊性质。有两边相等的三角形1. 等腰三角形两腰上的中线相等。2. 等腰三角形两腰上的高相等。EABCDE3. 等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。4. 等腰三角形两个底角的平分线相等。等腰三角形的两个底角相等。在同一个三角形中,等边对等角也可说成:3 、等边三角形的定义。三边都相等的三角形是等边三角形4 、等边三角形是特殊的等腰三角形,除具有等腰三角形的性质外,还具有特殊的性质吗?等边三角形的各角都都等于 60°2.3 等腰三角形的性质定理( 2 ) BD = CD, 即 AD 为底边上的中线 AD⊥BC , 即 AD 为底边上的高ADCB 如果已知 AB=AC,BAD=CAD(AD∠∠是顶角平分线 ). 那么有什么结论 ?如果已知 AB=AC,AD⊥BC(AD 是底边上的高 ).那么有什么结论 ?BD=CD(AD 是底边上的中线 ),∠BAD=∠CAD(AD 是顶角平分线 ). 等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合 .简称“等腰三角形三线合一”ADCB如果已知 AB=AC,BD=CD (AD 是底边上的中线 ). 那么有什么结论 ?ADBC(AD⊥是底边上的高 ), ∠BAD= CAD(AD∠是顶角平分线 )不是等腰三角形有没有这个特征呢?在△ ABC 中( 1 )∵ AB=AC , ADBC⊥,∴∠___=___∠, ____=____ ;( 2 )∵ AB=AC , AD 是中线,∴∠ _ =∠ _, ________⊥;( 3 )∵ AB=AC , AD 是角平分线,∴____⊥____ , ____=____ 。 CAB 12D等腰三角形“三线合一”的性质用符号语言表示为:12B D C D12ADBCADBCB D C DE1. 已知 : 如图 , 在△ ABC 中 ,AB = AC,AD⊥BC于点 D.E 为 AD 上的一点 ,EF⊥AB,EG⊥AC,F,G 分别为垂足 . 求证 :EF = EG.2 .如图,在△ ABC 中, AB = AC , ADBC⊥于 D. 若 AB = 5 , BD = 4 ,求△ ABC 的周长 .通过这堂课的学习,你得到了些什么?小结:等腰三角形⑵ 等腰三角形的顶角平分线、 底边上的中线和高互相重合, 简称等腰三角形三线合一。⑴ 等腰三角形的两个底角相等, 也就是说,在同一个三角形 中,等边对等角。 2. 等边三角形的各角都都等于 60°