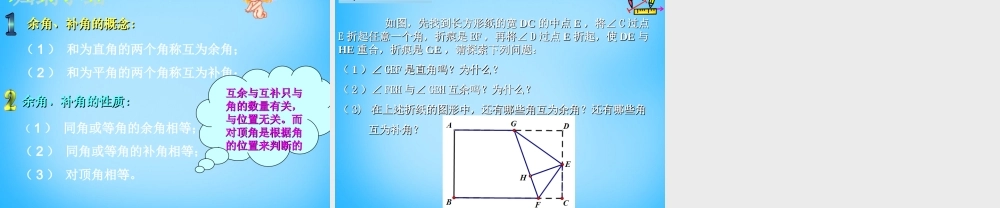
你知道吗?打台球的游戏中,你知道吗?打台球的游戏中,台球击到桌沿又反弹回来的路线,台球击到桌沿又反弹回来的路线,就象光的反射定律中入射光线与就象光的反射定律中入射光线与反射光线的路线是一样的。反射光线的路线是一样的。 下图中是一个经过改造的下图中是一个经过改造的台球桌面示意图,图中的阴影为台球桌面示意图,图中的阴影为66 个袋孔,如果一球按图示方向个袋孔,如果一球按图示方向击出去,最后落入第几个袋孔?击出去,最后落入第几个袋孔?1 .在具体情境中了解补角、余角的定义。2 .知道同角或等角的余角相等、同角或等角的补角相等,并能解决实际问题。3 .经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理表达的能力。1 、观察下列图形,你能发现∠∠ 11 和 ∠和 ∠ 22的关系吗?的关系吗?∠∠11 + ∠+ ∠ 22 =90=9000∠∠11 + ∠+ ∠ 22 =90=9000(( 11 )) 30 30 ,, 70 70 与与 80 80 的和为平角,所以这三个角互补( 的和为平角,所以这三个角互补( ) )(( 22 )一个角的余角必为锐角。 ( ))一个角的余角必为锐角。 ( )(( 33 )一个角的补角必为钝角。 ( ))一个角的补角必为钝角。 ( )(( 44 )) 90 90 的角为余角。 ( )的角为余角。 ( )(( 55 )两角是否互补既与其大小有关又与其位置有关( )两角是否互补既与其大小有关又与其位置有关( ) )00×√××× 互余与互补互余与互补是指是指两个角两个角之间的之间的数量关系数量关系,与它们,与它们的位置关系无关。的位置关系无关。判断下列说法是否正确判断下列说法是否正确0000002 、观察下列图形,你能发现∠∠ 11 和 ∠和 ∠ 22的关系吗?的关系吗?∠∠11 + ∠+ ∠ 22 =180=18000∠∠11 + ∠+ ∠ 22 =180=180001. 1. 下列哪些角互为余角?有相等的角吗?下列哪些角互为余角?有相等的角吗?∠∠11 与∠与∠ 44 ,∠,∠ 22 与与∠∠ 33∠∠11 与∠与∠ 33 ,,∠∠ 22 与与∠∠ 44∠∠3= 4∠3= 4∠∠∠11 与∠与∠ 22 ,∠,∠ 22 与与∠∠ 33∠∠1= 3∠1= 3∠☞☞ 如图,有一破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?为什么?4000 方法一:可利用对顶角相等得出。方法二:可利用补角得出。3344...