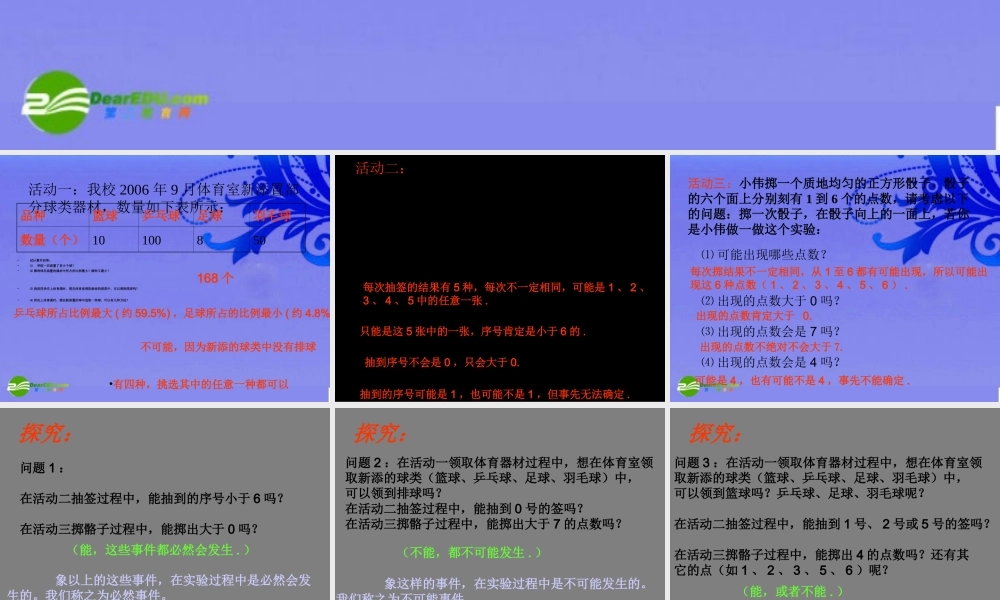
第 25 章 概 率25.1.1 随机事件 活动一:我校 2006 年 9 月体育室新添置部分球类器材,数量如下表所示:•试计算并回答:•⑴ 学校一共添置了多少个球?•⑵ 哪种球在添置的器材中所占的比例最大?哪种又最小?•⑶ 我班同学在上体育课时,想在体育室领取新添的球类中,可以领到排球吗?•⑷ 若在上体育课时,想在新添置的球中选取一种球,可以有几种方法?品种篮球乒乓球足球羽毛球数量(个) 10100850168 个乒乓球所占比例最大 ( 约 59.5%) ,足球所占的比例最小 ( 约 4.8%)不可能,因为新添的球类中没有排球•有四种,挑选其中的任意一种都可以 活动二:5名同学参加讲演比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状大小、完全相同的纸签,上面分别标有出场的序号1、2、3、4、5,小军首先抽签,他在看不到纸签上数字的情况下从筒中随机(任意)地取一根纸签,请考虑以下问题:⑴ 抽到的序号有几种可能情况?⑵ 抽到的序号小于 6 吗?⑶ 抽到的序号会是 0 吗?⑷ 抽到的序号是 1 吗?每次抽签的结果有 5 种,每次不一定相同,可能是 1 、 2 、3 、 4 、 5 中的任意一张 .只能是这 5 张中的一张,序号肯定是小于 6 的 .抽到序号不会是 0 ,只会大于 0.抽到的序号可能是 1 ,也可能不是 1 ,但事先无法确定 . 活动三:小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有 1 到 6 个的点数,请考虑以下的问题:掷一次骰子,在骰子向上的一面上,若你是小伟做一做这个实验:⑴ 可能出现哪些点数?⑵ 出现的点数大于 0 吗?⑶ 出现的点数会是 7 吗?⑷ 出现的点数会是 4 吗?每次掷结果不一定相同,从 1 至 6 都有可能出现,所以可能出现这 6 种点数( 1 、 2 、 3 、 4 、 5 、 6 ) .出现的点数肯定大于 0.出现的点数不绝对不会大于 7. 可能是 4 ,也有可能不是 4 ,事先不能确定 .探究:问题 1 :在活动二抽签过程中,能抽到的序号小于 6 吗?在活动三掷骼子过程中,能掷出大于 0 吗?(能,这些事件都必然会发生 . ) 象以上的这些事件,在实验过程中是必然会发生的。我们称之为必然事件。问题 2 :在活动一领取体育器材过程中,想在体育室领取新添的球类(篮球、乒乓球、足球、羽毛球)中,可以领到排球吗?在活动二抽签过程中,能抽到 0 号的签吗?在活动三掷骼子过程中,能掷出大于 7 的点数吗?...