三角函数章复习 高三数学上学期期中考试复习课件集 人教版 高三数学上学期期中考试复习课件集 人教版VIP免费

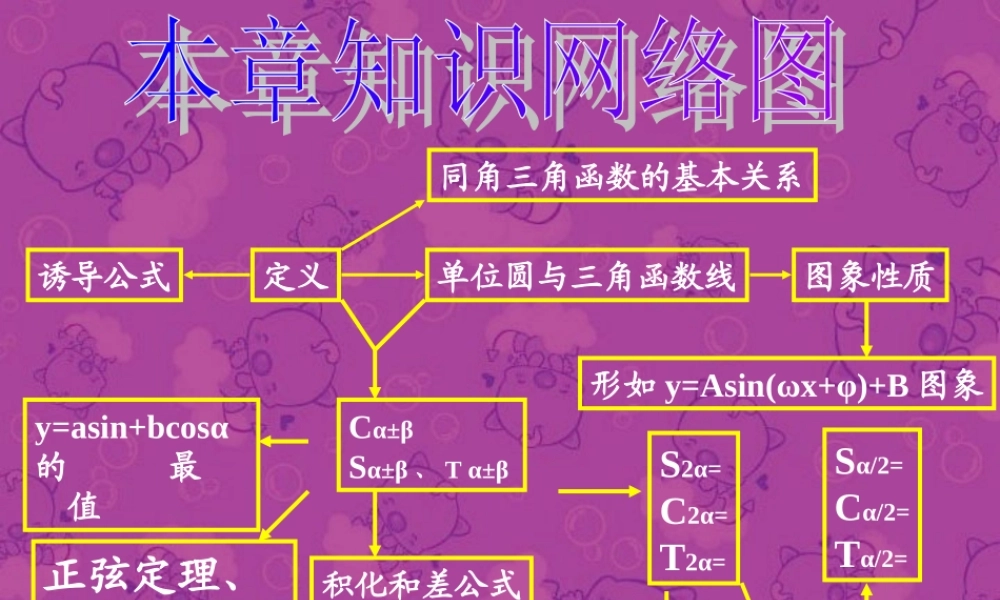
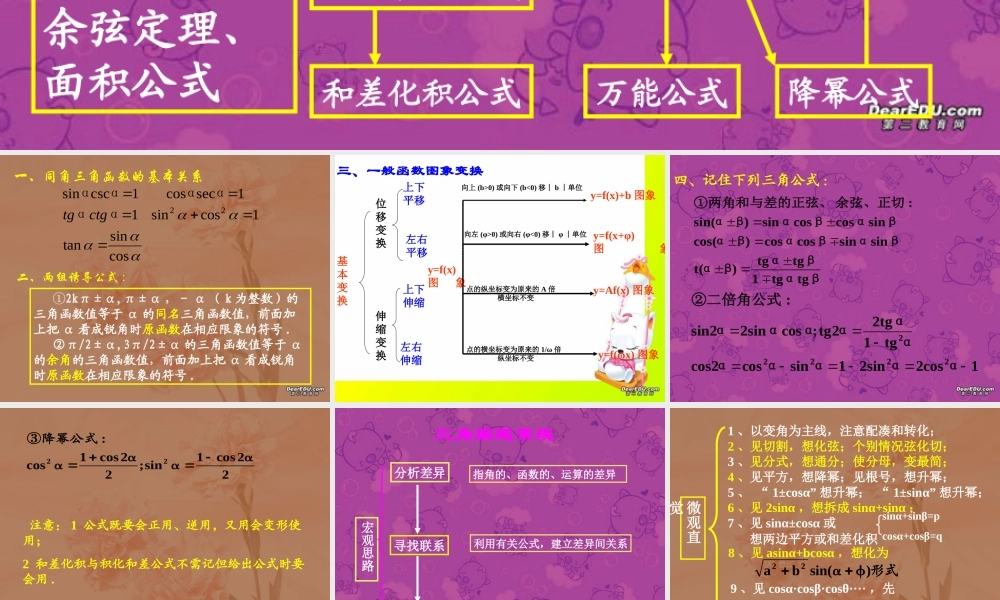
定义同角三角函数的基本关系图象性质单位圆与三角函数线诱导公式Cα±βSα±β 、 T α±β y=asin+bcosα的 最 值形如 y=Asin(ωx+φ)+B 图象万能公式和差化积公式积化和差公式Sα/2=Cα/2=Tα/2=S2α=C2α=T2α=正弦定理、余弦定理、面积公式降幂公式一、同角三角函数的基本关系cossintan1cossin11seccos1cscsin22ααααααctgtg二、两组诱导公式 : ①2kπ±α,π±α ， - α （ k 为整数）的三角函数值等于 α 的同名三角函数值，前面加上把 α 看成锐角时原函数在相应限象的符号 . ②π/2±α,3π/2±α 的三角函数值等于 α的余角的三角函数值，前面加上把 α 看成锐角时原函数在相应限象的符号 .三、一般函数图象变换基本变换位移变换伸缩变换上下平移左右平移上下伸缩左右伸缩y=f(x)图 象y=f(x)+b 图象y=f(x+φ)图 象y=Af(x) 图象 y=f(ωx) 图象向上 (b>0) 或向下 (b<0) 移︱ b ︱单位向左 (φ>0) 或向右 (φ<0) 移︱ φ ︱单位点的横坐标变为原来的 1/ω 倍 纵坐标不变点的纵坐标变为原来的 A 倍 横坐标不变四、记住下列三角公式 :βαβαβαβαβαβαβαβαβα余弦、正切①两角和与差的正弦、tgtg1tgtg)(tsinsincoscos)cos(sincoscossin )sin(:1cos2sin21sincoscos2tg1tg22tg;cos2sin sin2:22222ααααααααααα②二倍角公式22cos1sin;22cos1cos:22αααα③降幂公式 注意： 1 公式既要会正用、逆用，又用会变形使用；2 和差化积与积化和差公式不需记但给出公式时要会用 .三角解题常规宏观思路分析差异寻找联系促进转化指角的、函数的、运算的差异利用有关公式，建立差异间关系活用公式，差异转化，矛盾统一1 、以变角为主线，注意配凑和转化；2 、见切割，想化弦；个别情况弦化切；3 、见分式，想通分；使分母，变最简；4 、见平方，想降幂；见根号，想升幂；5 、 “ 1±cosα” 想升幂； “ 1±sinα” 想升幂；6 、见 2sinα ，想拆成 sinα+sinα ；7 、见 sinα±cosα 或想两边平方或和差化积8 、见 asinα+bcosα ，想化为形式φα)sin(ba229 、见 cosα·cosβ·cosθ···· ，先ααα运用sin22sincos若不行，则化和差微观直觉sinα+sinβ=pcosα+cosβ=q..D;.C;.B;.A)(22cos2cos)90(1第四象限第三象限第二象限第－象限角属于α则，α...