数学 2.3 数学归纳法2课件 新人教A版选修2-2 课件VIP免费

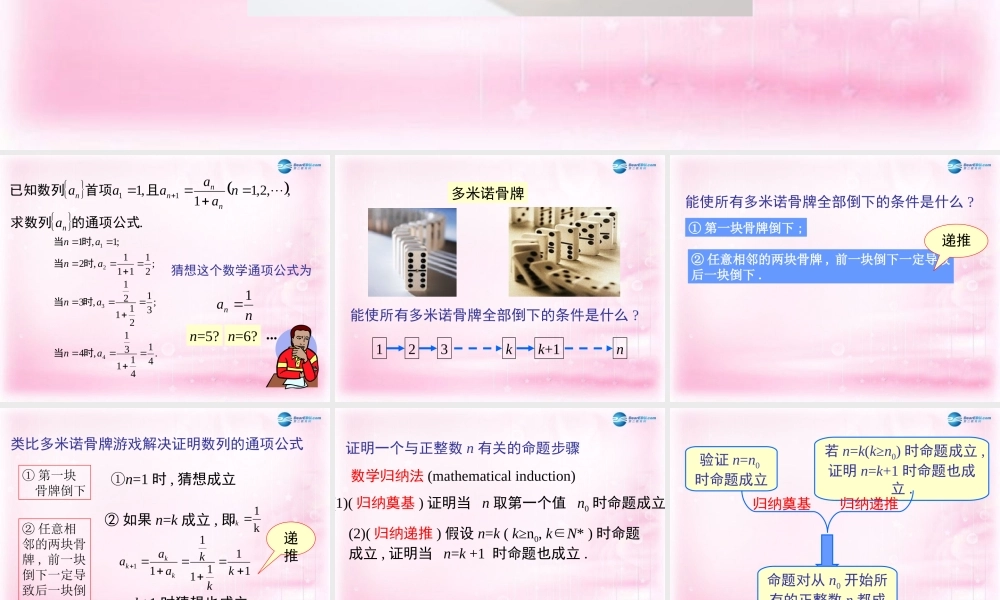
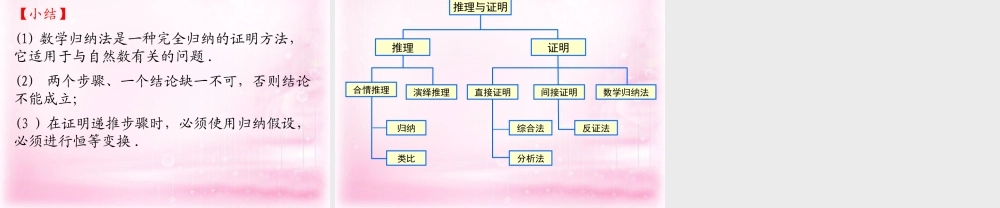
数学归纳法  .,,2,11,111的通项公式求数列且首项已知数列nnnnnanaaaaa.4141131,4;3121121,3;21111 ,2;1,14321anananan时当时当时当时当猜想这个数学通项公式为nan1n=5? n=6? ...多米诺骨牌能使所有多米诺骨牌全部倒下的条件是什么 ?123kk+1n能使所有多米诺骨牌全部倒下的条件是什么 ?① 第一块骨牌倒下 ;② 任意相邻的两块骨牌 , 前一块倒下一定导致后一块倒下 .递推① 第一块 骨牌倒下② 任意相邻的两块骨牌 , 前一块倒下一定导致后一块倒下 .①n=1 时 , 猜想成立② 如果 n=k 成立 , 即k1ka1111111kkkaaakkkn=k+1 时猜想也成立类比多米诺骨牌游戏解决证明数列的通项公式递推nan1数列通公式为证明一个与正整数 n 有关的命题步骤(1)( 归纳奠基 ) 证明当 n 取第一个值 n0 时命题成立 ;(2)( 归纳递推 ) 假设 n=k ( k≥n0, k∈N* ) 时命题成立 , 证明当 n=k +1 时命题也成立 .数学归纳法 (mathematical induction)验证 n=n0时命题成立若 n=k(k≥n0) 时命题成立 ,证明 n=k+1 时命题也成立 .归纳奠基归纳递推命题对从 n0 开始所有的正整数 n 都成立例 1 用数学归纳法证明*222612121Nnnnnn证明 :(1) 当 n=1 时 , 左边 =12=1 左边右边16112111(2) 假设当 n=k 时等式成立 , 即,612121222kkkk 216121kkkk2222121kk667212kkk6161212kkkk63221kkk 6112211kkk即当 n=k +1 时等式也成立根据 (1) 和 (2), 可知等式任何 nN* 都成立在第二步时先“凑”出 n=k 的形式，再“凑”出 n=k+1的目标式.,,,,,,,,13231,,1071,741,411.24321明并用数学归纳法进行证的表达式猜想根据计算结果计算已知数列例nSSSSSnn123411112=,=,1 4444 77213314=,=,77 10101010 131331.31nSSSSnnnnSn  解：可以看到，上面四个结果的分数中，分子与项数 一致，分母可用项数 表示为，于是可以猜想 11111,=,.43 1 141111++1 44 77 1032313111111++1 44 77 10323131 3413131 34nSnkkkkkkkkkk...