九年级数学(新高一)暑假辅导数学讲义 高次方程、分式方程、无理方程的解法课件 人教新课标版 课件VIP免费

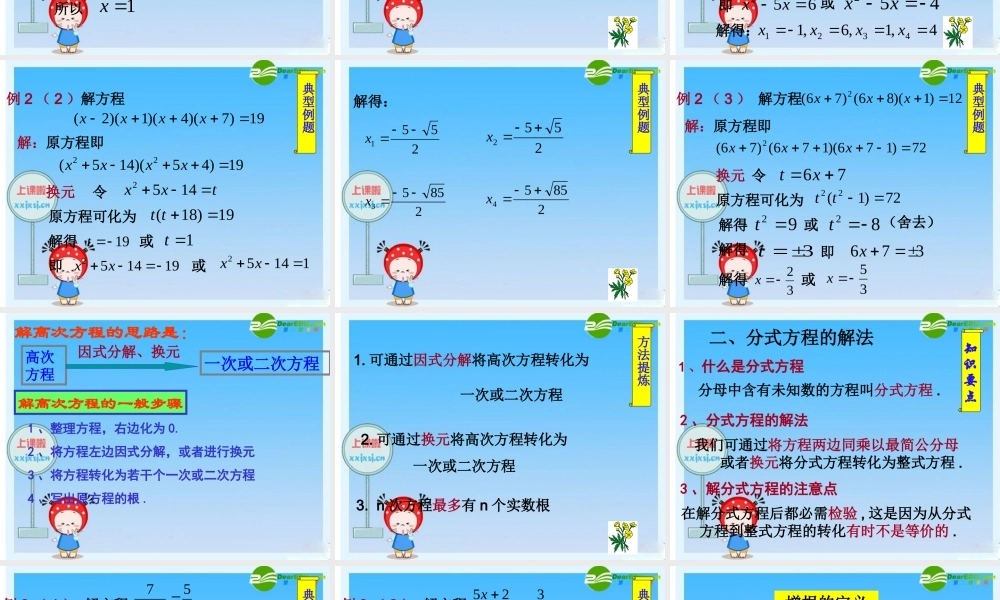
高次方程、分式方程、无理方程的解法新高一数学 高次方程、分式方程、无理方程的解法 内容概况内容概况 无理方程 高次方程 分式方程一次或二次方程 整式方程有理方程 因式分解、 换元两边同乘以最简公分母、 换元两边平方、换元 2 、高次方程的解法 我们可通过因式分解和换元将一元高次方程 转化为一元一次方程和一元二次方程 一、高次方程的解法知识要点知识要点 一 . 高次方程的解法1 、什么是高次方程 整式方程中，未知数的次数大于或等于 3的方程称为高次方程 典型例题03423xxx0)34(2xxx0)3)(1(xxx所以例 1 （ 1 ）解方程 解：因式分解 3,1,0321xxx高次方程的解法例题1 （ 1 ） 典型例题013x043)21(122xxx0)1)(1(123xxxx因为 所以 01 x所以 例 1 （ 2 ）解方程 解： 因式分解1x 典型例题高次方程解法例 1 （ 3 ）例 1 （ 3 ） 解方程084223xxx解：因式分解0)2(4)2(2xxx0)2)(4(2xx0)2)(2(2 xx所以2,2321xxx 典型例题高次方程解法例 2(1)例 2 （ 1 ）解 方 程024)5(2)5(222xxxx解：换元 令 xxt52 则原方程可以化为 02422tt即 0)4)(6(tt 故 6t或4t即 652xx或 452xx解得： 4,1,6,14321xxxx 典型例题高次方程解法例 2 （ 2 ）例 2 （ 2 ）解方程 19)7)(4)(1)(2(xxxx22(514)(54)19xxxx解：原方程即 换元 令 2514xxt原方程可化为 19)18(tt解得 19t或 1t即 251419xx或 25141xx 典型例题高次方程解法例 2 （ 2 ）解得： 2551x2552x28553x28554x 典型例题高次方程解法例 2 （ 3 ）例 2 （ 3 ） 解方程解：原方程即 换元 令 原方程可化为 解得 或 即 12)1)(86()76(2xxx72)176)(176()76(2xxx76  xt72)1( 22tt92 t82t（舍去）3t解得 376x32x或 35x解得 解高次方程的一般步骤 1 、整理方程，右边化为 0. 2 、将方程左边因式分解，或者进行换元 3 、将方程转化为若干个一次或二次方程 4 、写出原方程的根 .解高次方程的思路是：高次方程一次或二次方程因式分解、换元 方法提炼高次方程解法方法提炼1. 可通过因式分解将高次方程...