八年级数学下册 16.1.2 分式基本性质(1)课件 人教新课标版 课件VIP免费

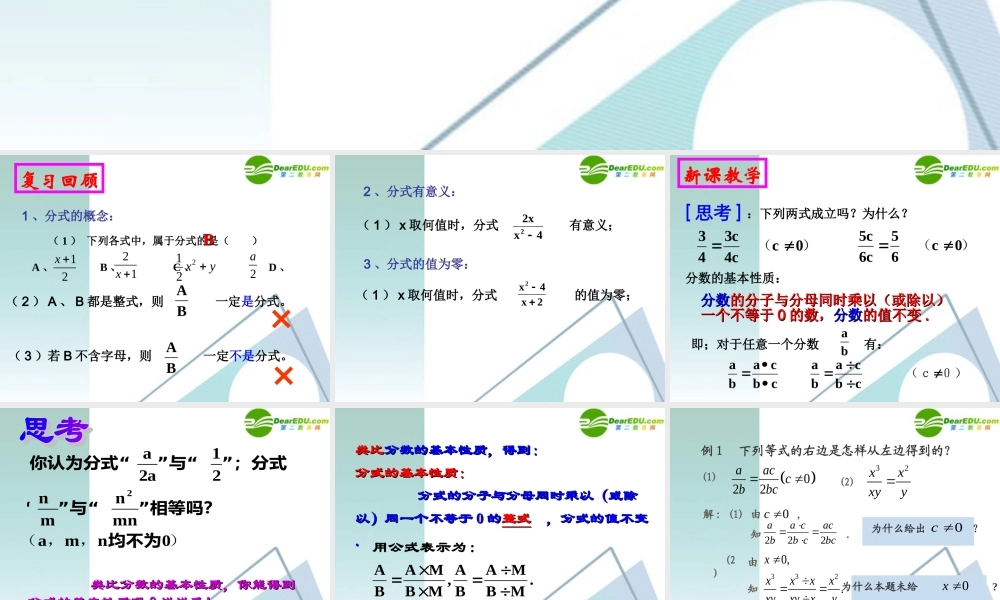
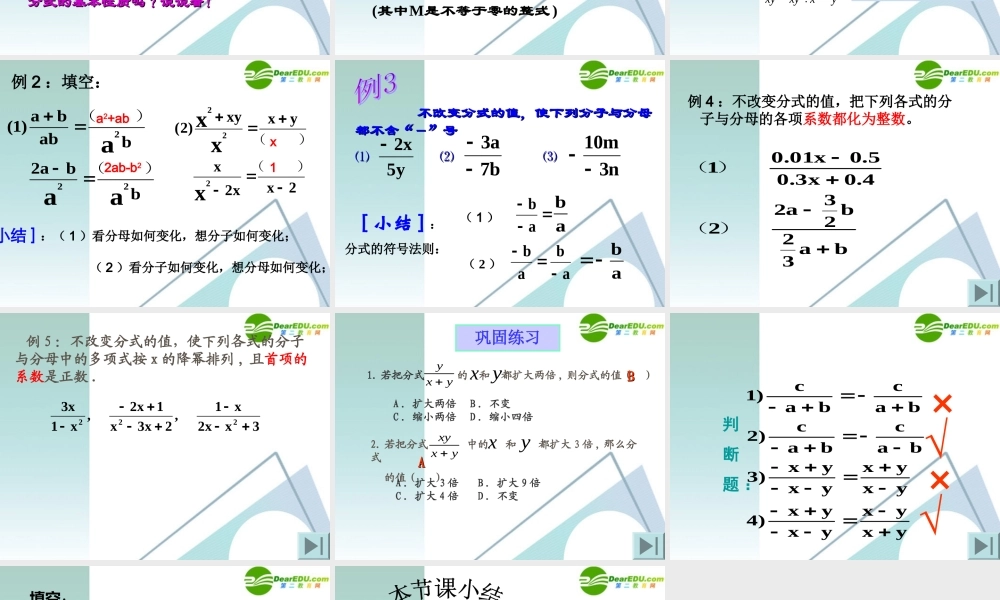
复习回顾1 、分式的概念： （ 1 ） 下列各式中，属于分式的是（ ） A 、 B 、 C 、 D 、12x 21x 2a212 xyBB（ 2 ） A 、 B 都是整式，则 一定是分式。BA（ 3 ）若 B 不含字母，则 一定不是分式。BA××2 、分式有意义：3 、分式的值为零：（ 1 ） x 取何值时，分式 有意义；4xx22 （ 1 ） x 取何值时，分式 的值为零；2x4x2新课教学[ 思考 ] ：下列两式成立吗？为什么？）0 c（c4c343）0 c（65c6c5分数分数的分子与分母同时乘以（或除以）的分子与分母同时乘以（或除以）一个不等于一个不等于 00 的数，的数，分数分数的值不变的值不变 ..分数的基本性质：０） （ｃcbcaba cbcaba即；对于任意一个分数 有：ba）0amn（ ，，mnnmn21a2a2均不为”相等吗？”“与“”；分式”“与“你认为分式 类比分数的基本性质，你能得到类比分数的基本性质，你能得到分式的基本性质吗？说说看！分式的基本性质吗？说说看！类比类比分数的基本性质，得到：分数的基本性质，得到：分式的基本性质：分式的基本性质： 分式的分子与分母同时乘以（或除分式的分子与分母同时乘以（或除以）同一个不等于以）同一个不等于 00 的的整式整式 ，分式的值不变 ，分式的值不变..)M(.MBMABA,MBMABA:是不等于零的整式其中用公式表示为例 1 下列等式的右边是怎样从左边得到的？(1)022aaccbbc 为什么给出 ?0c  由 , 知 .0c 222aa cacbb cbc32xxxyy(2)为什么本题未给 ?0x (2)解 : (1)由知3320,.xxxxxxyxyxy例 2 ：填空：b （）ba2 b （）abba)1(aaa2222x （）x2x （）yxxy)2(xxx222a2+ab2ab-b2x1[ 小结 ] ：（ 1 ）看分母如何变化，想分子如何变化； （ 2 ）看分子如何变化，想分母如何变化； 不改变分式的值，使下列分子与分母不改变分式的值，使下列分子与分母都不含“－”号 都不含“－”号 ⑴⑵⑶ ⑴⑵⑶y5x2b7a3n3m10 [ 小结 ] ：分式的符号法则：ababab（ 2 ）abab（ 1 ）例 4 ：不改变分式的值，把下列各式的分子与分母的各项系数都化为整数。ba32b23a2 ）2（4.0x3.05.0x01.0 ）1（3xx2x1 ,2x3x1x2 ,x1x3222例 5 ：不改变分式的值，使下列各式的分子与分母中的多项式按 x 的降幂排列 , 且首项...