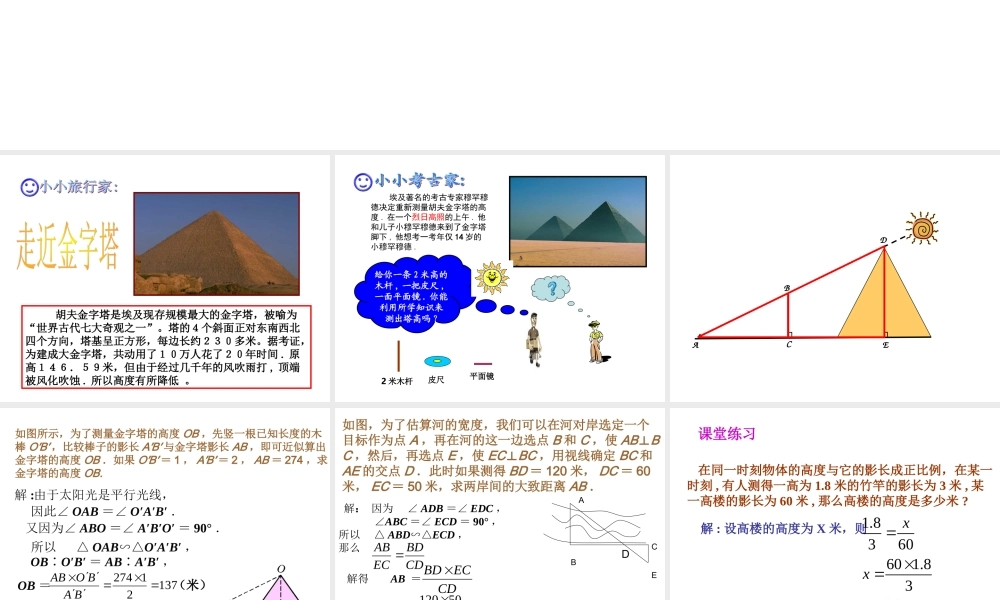
相似三角形的应用 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间 . 原高146.59米,但由于经过几千年的风吹雨打 , 顶端被风化吹蚀 . 所以高度有所降低 。 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度 . 在一个烈日高照的上午 . 他和儿子小穆罕穆德来到了金字塔脚下 , 他想考一考年仅 14 岁的小穆罕穆德 .给你一条 2 米高的木杆 , 一把皮尺 ,一面平面镜 . 你能利用所学知识来测出塔高吗 ?2 米木杆皮尺平面镜 ACBDE┐┐ 图 18.3.12 如图所示,为了测量金字塔的高度 OB ,先竖一根已知长度的木棒 O′B′ ,比较棒子的影长 A′B′ 与金字塔影长 AB ,即可近似算出金字塔的高度 OB .如果 O′B′ = 1 , A′B′ = 2 , AB = 274 ,求金字塔的高度 OB. 13721274BABOAB即该金字塔高为 137 米. (米)解 :由于太阳光是平行光线,因此∠ OAB =∠ O′A′B′ .又因为∠ ABO =∠ A′B′O′ = 90° .所以 △ OAB∽△O′A′B′ ,OB∶O′B′ = AB∶A′B′ ,OB = 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点 A ,再在河的这一边选点 B 和 C ,使 AB⊥BC ,然后,再选点 E ,使 EC⊥BC ,用视线确定 BC 和AE 的交点 D .此时如果测得 BD = 120 米, DC = 60米, EC = 50 米,求两岸间的大致距离 AB . 解: 因为 ∠ ADB =∠ EDC , ∠ABC =∠ ECD = 90° , 所以 △ ABD∽△ECD , 那么 CDBDECAB 解得AB =CDECBD =6050120= 100 (米). 答: 两岸间的大致距离为 100 米.DABCE 在同一时刻物体的高度与它的影长成正比例,在某一时刻 , 有人测得一高为 1.8 米的竹竿的影长为 3 米 , 某一高楼的影长为 60 米 , 那么高楼的高度是多少米 ?课堂练习解 : 设高楼的高度为 X 米,则1.836060 1.8336xxx答 : 楼高 36 米 . 课堂小结 :一 、相似三角形的应用主要有如下两个方面 1 测高 ( 不能直接使用皮尺或刻度尺量的 ) 2 测距 ( 不能直接测量的两点间的距离 )贰 、测高的方法 测量不能到达顶部的物体的高度 , 通常用“在同一时刻物高与影长的比例”的原理解决 叁 、测距的方法 测量不能到达两点间的距离 , 常构造相似三角形求解