九年级数学上册 次函数的图象 课件 北京课改版 课件VIP免费

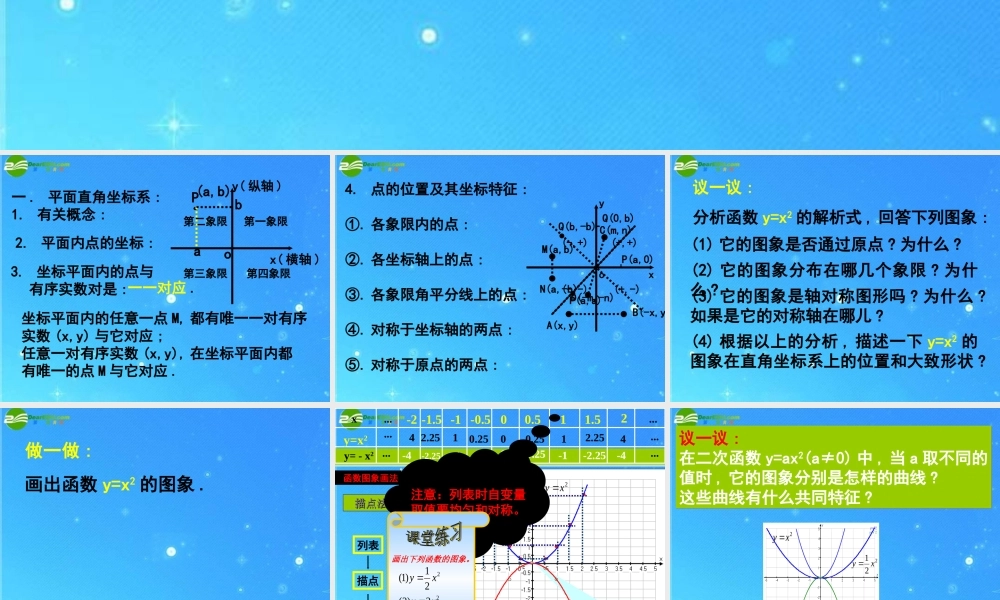
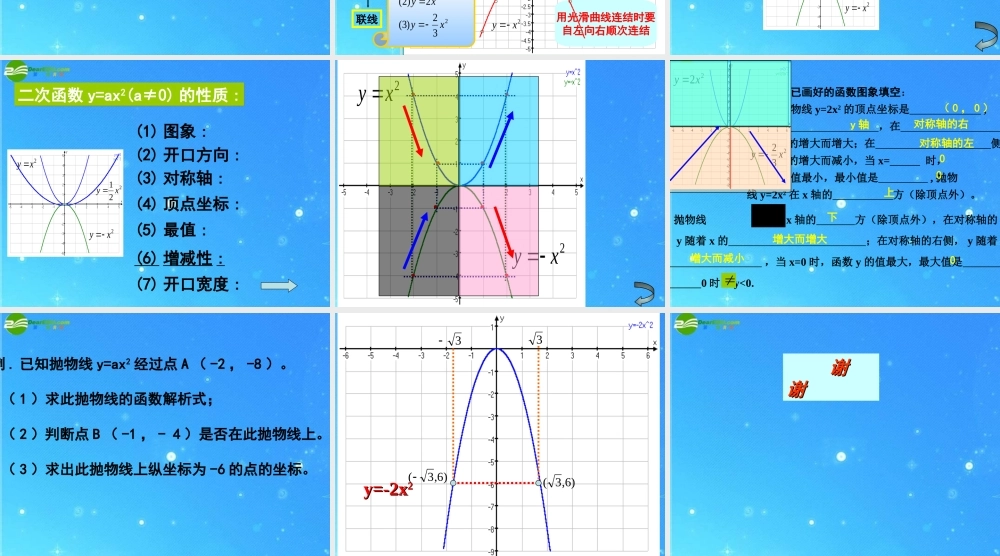
一 . 平面直角坐标系 :1. 有关概念 :x( 横轴 )y( 纵轴 )o第一象限第二象限第三象限第四象限Pab(a,b)2. 平面内点的坐标 :3. 坐标平面内的点与 有序实数对是 :一一对应 .坐标平面内的任意一点 M, 都有唯一一对有序实数 (x,y) 与它对应 ;任意一对有序实数 (x,y), 在坐标平面内都有唯一的点 M 与它对应 . 4. 点的位置及其坐标特征 :①. 各象限内的点 :②. 各坐标轴上的点 :③. 各象限角平分线上的点 :④. 对称于坐标轴的两点 :⑤. 对称于原点的两点 :xyo(+,+)(-,+)(-,-)(+,-)P(a,0)Q(0,b)P(a,a)Q(b,-b)M(a,b)N(a,-b)A(x,y) B(-x,y)C(m,n)D(-m,-n) 议一议 :分析函数 y=x2 的解析式 , 回答下列图象 :(1) 它的图象是否通过原点 ? 为什么 ?(2) 它的图象分布在哪几个象限 ? 为什么 ?(3) 它的图象是轴对称图形吗 ? 为什么 ?如果是它的对称轴在哪儿 ?(4) 根据以上的分析 , 描述一下 y=x2 的图象在直角坐标系上的位置和大致形状 ? 做一做 :画出函数 y=x2 的图象 . xy=x2y= - x2..................0-2 -1.5 -1 -0.511.50.52 函数图象画法列表描点联线00.2512.2540.2512.254 描点法描点法用光滑曲线连结时要自左向右顺次连结0-0.25-1-2.25-4-0.25-1-2.25-4注意：列表时自变量取值要均匀和对称。2xy 2xy画出下列函数的图象。22232)3(2)2(21)1(xyxyxy 议一议 :在二次函数 y=ax2(a≠0) 中 , 当 a 取不同的值时 , 它的图象分别是怎样的曲线 ?这些曲线有什么共同特征 ?议一议 :在二次函数 y=ax2(a≠0) 中 , 当 a 取不同的值时 , 它的图象分别是怎样的曲线 ?这些曲线有什么共同特征 ?2xy 2xy221 xy  二次函数 y=ax2(a≠0) 的性质 :二次函数 y=ax2(a≠0) 的性质 :(1) 图象 :(2) 开口方向 :(3) 对称轴 :(4) 顶点坐标 :(5) 最值 :(6) 增减性 :(7) 开口宽度 :2xy 2xy221 xy  2xy 2xy 根据左边已画好的函数图象填空：（ 1 ）抛物线 y=2x2 的顶点坐标是 ,对称轴是 ，在 侧，y 随着 x 的增大而增大；在 侧，y 随着 x 的增大而减小，当 x= 时，函数 y 的值最小，最小值是 , 抛物线 y=2x2 在 x 轴的 方（除顶点外）。22xy 232 xy（ 2 ）抛物线 在 x 轴的 方（除顶点外），在对称轴的左侧， y 随着 x 的 ；在对称轴的右侧， y 随着 x 的 ，当 x=0 时，函数 y 的值最大，最大值是 ，当 x 0 时， y<0.232 xy（ 0 ， 0 ）y 轴对称轴的右对称轴的左00上下增大而增大增大而减小0 例 . 已知抛物线 y=ax2 经过点 A （ -2 ， -8 ）。 （ 1 ）求此抛物线的函数解析式； （ 2 ）判断点 B （ -1 ， - 4 ）是否在此抛物线上。 （ 3 ）求出此抛物线上纵坐标为 -6 的点的坐标。 y=-2xy=-2x2233)6,3()6,3( 谢 谢 谢谢