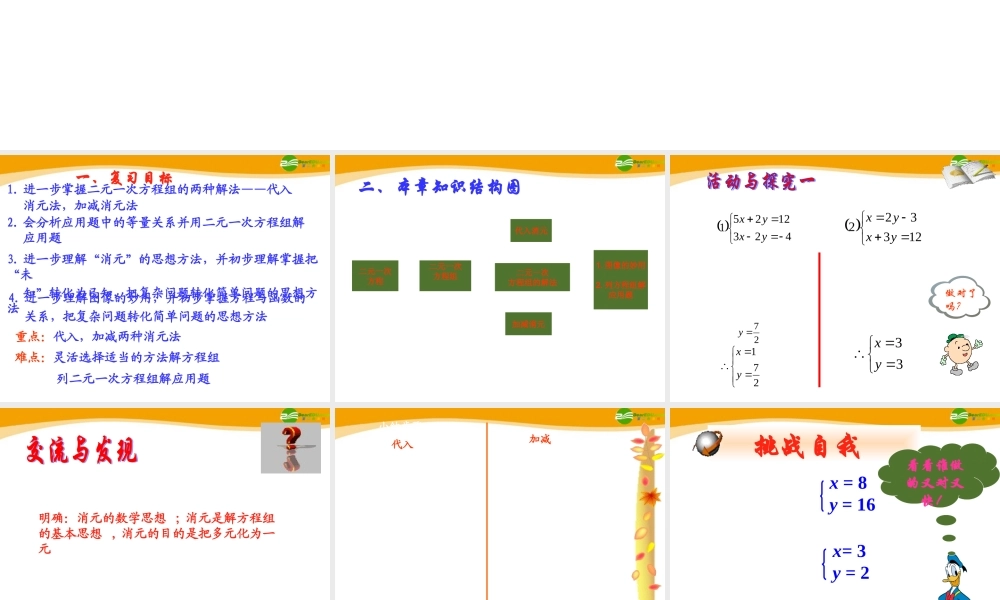
泰山出版社数学学科七年级下学期复习多媒体教学课件 复习课一、复习目标1. 进一步掌握二元一次方程组的两种解法——代入 消元法,加减消元法2. 会分析应用题中的等量关系并用二元一次方程组解 应用题3. 进一步理解“消元”的思想方法,并初步理解掌握把“未 知”转化为已知,把复杂问题转化简单问题的思想方法重点:代入,加减两种消元法难点:灵活选择适当的方法解方程组列二元一次方程组解应用题 4. 进一步理解图像的妙用,并初步掌握方程与函数的 关系,把复杂问题转化简单问题的思想方法二、本章知识结构图二元一次方程二元一次方程组代入消元二元一次方程组的解法加减消元1. 图像的妙用2. 列方程组解应用题1 、先观察下列方程组用什么方法消去未知数好 , 并解下列方程组 42312251yxyx 123322yxyx①②①②解:①+②8x=8x=1③把③代入①得27y271yx解:把①代入②得2y-3+3y=125y=15y=3③把③代入①得 x=333yx做对了吗?1 、解二元一次方程组的基本思想是什么?2 、代入法,加减法解二元一次方程组的一般步骤明确:消元的数学思想 ; 消元是解方程组的基本思想 , 消元的目的是把多元化为一元小结步骤 :(2) 加减消去一元 ,得一元一次方程(3) 解这个一元一次方程 , 求得一个未知数的值(4) 把求得的未知数的值代入方程组中任意一个方程 , 即可得另一个未知数的值 .(5) 作结论(1) 设法使方程组两个方程某一未知数系数相等或相反 加减代入(1) 将方程组中某一方程变形成用一个未知数的代数式表示另一个未知数(2) 将变形后的方程代入另一个方程消去一个未知数得一个一元一次方程(3) 解这个一元一次方程求出一个未知数的值(4) 把求得的未知数的值代入变形好的方程中 , 即可得另一个未知数的值 .(5) 作结论 挑战自我看看谁做的又对又快!2x+y=32 ① 2x-y=0 ② 1.2.3x-2y=5 ①x+3y=9 ②x = 8y = 16x= 3y = 22. 一项工程,甲乙两人合做 8 天可完成任务,需费用 3520 元,若甲独 做 6 天后,剩下的工程由乙独做,还需 12 天才能完成,这样的费用 需 3480 元问( 1 )甲乙两人单独完成 这项工程每天各需要费用多少元?( 2 )甲乙两人单独完成 这项工程各需要多少时间?分析:工程问题常用的等量关系有 工作量=工作效率 × 工作时间 各个部分工程量之和=总工作量解[ 1 ]:设甲乙两人单独完成 ...