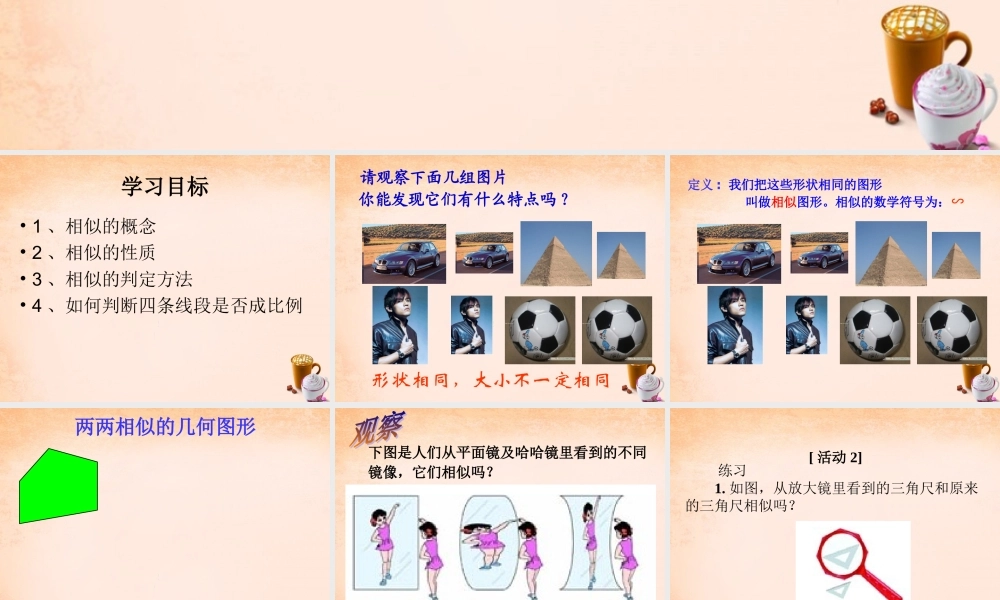
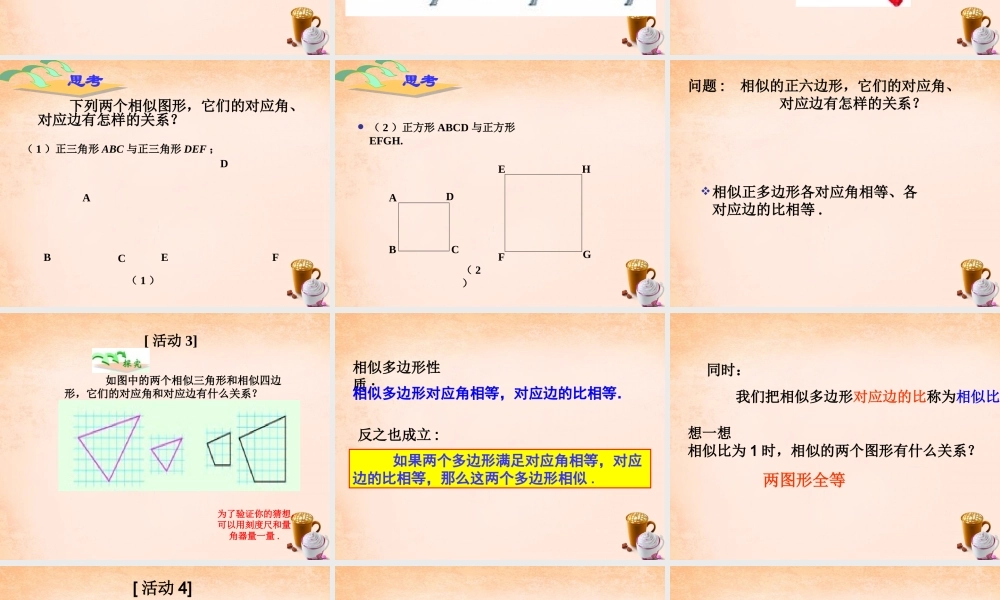
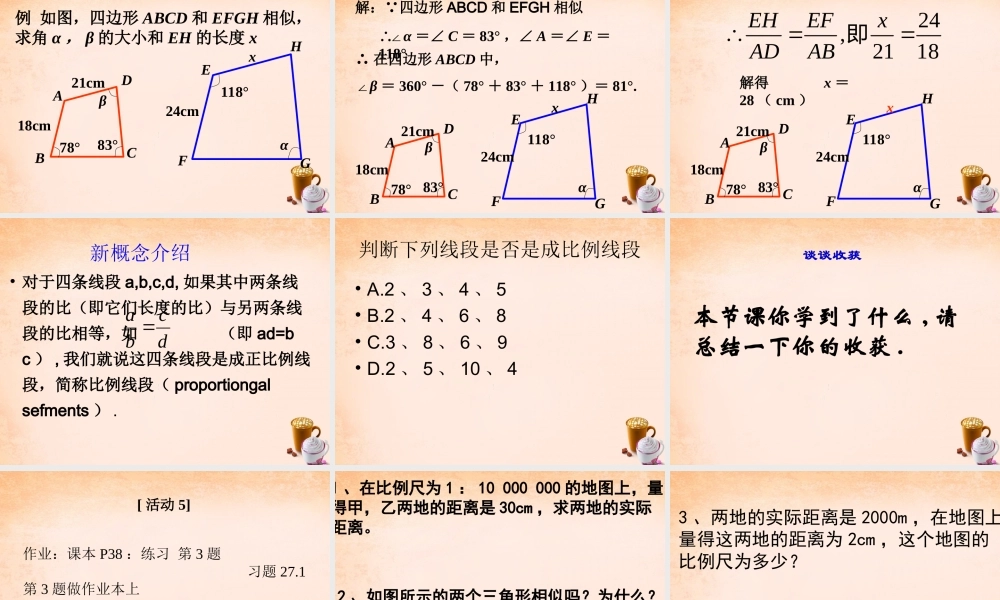
§27.1 图形的相似学习目标• 1 、相似的概念• 2 、相似的性质• 3 、相似的判定方法• 4 、如何判断四条线段是否成比例请观察下面几组图片你能发现它们有什么特点吗 ?形状相同,大小不一定相同定义 : 我们把这些形状相同的图形 叫做相似图形。相似的数学符号为:∽两两相似的几何图形下图是人们从平面镜及哈哈镜里看到的不同镜像,它们相似吗? 练习 1. 如图,从放大镜里看到的三角尺和原来的三角尺相似吗? [ 活动 2] 下列两个相似图形,它们的对应角、对应边有怎样的关系?( 1 )正三角形 ABC 与正三角形 DEF ;( 1 )BCDEFA思考 ( 2 )正方形 ABCD 与正方形EFGH. BCDA( 2)EFHG思考问题 : 相似的正六边形,它们的对应角、 对应边有怎样的关系?相似正多边形各对应角相等、各对应边的比相等 . 如图中的两个相似三角形和相似四边形,它们的对应角和对应边有什么关系?为了验证你的猜想,可以用刻度尺和量角器量一量 .[ 活动 3]相似多边形性质 :相似多边形对应角相等,对应边的比相等. 如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似 .反之也成立 : 同时: 我们把相似多边形对应边的比称为相似比.两图形全等想一想相似比为 1 时,相似的两个图形有什么关系?[ 活动 4]例 如图,四边形 ABCD 和 EFGH 相似,求角 α , β 的大小和 EH 的长度 xDABC18cm21cm78°83°β24cmGEFHαx118°DABC18cm21cm78° 83°β24cmGEFHαx118°∴ 在四边形 ABCD 中,∠β = 360° -( 78° + 83° + 118° )= 81°.∴∠α =∠ C = 83° ,∠ A =∠ E =118°解: 四边形 ABCD 和 EFGH 相似DABC18cm21cm78° 83°β24cmGEFHαx118°解得 x =28 ( cm )24,2118EHEFxADAB即新概念介绍• 对于四条线段 a,b,c,d, 如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即 ad=bc ) , 我们就说这四条线段是成正比例线段,简称比例线段( proportiongal sefments ) . dcba 判断下列线段是否是成比例线段• A.2 、 3 、 4 、 5• B.2 、 4 、 6 、 8• C.3 、 8 、 6 、 9• D.2 、 5 、 10 、 4谈谈收获本节课你学到了什么 , 请总结一下你的收获 .[ 活动 5]作业:课本 P38 :练习 第 3 题 习题 27.1第 3 题做作业本上 附加 : 《分层...