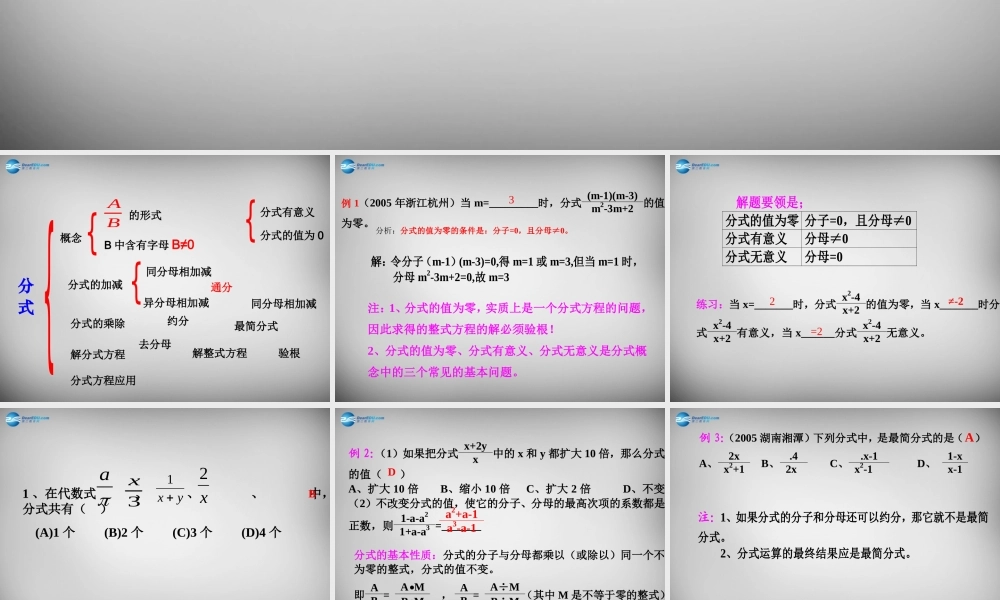
新人教版八 ( 上 ) 第 15 章分式课件总复习课件{{分式{分式有意义分式的值为 0{同分母相加减异分母相加减概念AB 的形式B 中含有字母 B≠0分式的加减分式的乘除通分约分最简分式解分式方程去分母解整式方程验根分式方程应用同分母相加减例 1(2005 年浙江杭州)当 m=_________时,分式 (m-1)(m-3) m2-3m+2 的值为零。 分析:分式的值为零的条件是:分子=0,且分母≠0。 解:令分子(m-1)(m-3)=0,得 m=1 或 m=3,但当 m=1 时, 分母 m2-3m+2=0,故 m=3 注:1、分式的值为零,实质上是一个分式方程的问题,因此求得的整式方程的解必须验根! 2、分式的值为零、分式有意义、分式无意义是分式概念中的三个常见的基本问题。 3解题要领是; 分式的值为零 分子=0,且分母≠0 分式有意义 分母≠0 分式无意义 分母=0 练习:当 x=_______时,分式 x2-4 x+2 的值为零,当 x_______时分式 x2-4 x+2 有意义,当 x______分式 x2-4 x+2 无意义。 2≠-2=21 、在代数式 、 、 、 中,分式共有( ) (A)1 个 (B)2 个 (C)3 个 (D)4 个3xx2ayx 1B例 2:(1)如果把分式 x+2y x 中的 x 和 y 都扩大 10 倍,那么分式的值( ) A、扩大 10 倍 B、缩小 10 倍 C、扩大 2 倍 D、不变 (2)不改变分式的值,使它的分子、分母的最高次项的系数都是正数,则 1-a-a2 1+a-a3 =_______ 分式的基本性质:分式的分子与分母都乘以(或除以)同一个不为零的整式,分式的值不变。 即 A B = A•M B•M , A B = A÷M B÷M (其中 M 是不等于零的整式) D a2+a-1 a3-a-1 例 3:(2005 湖南湘潭)下列分式中,是最简分式的是( ) A、 2x x2+1 B、 .4 2x C、 .x-1 x2-1 D、 1-x x-1 注:1、如果分式的分子和分母还可以约分,那它就不是最简分式。 2、分式运算的最终结果应是最简分式。 A例 4:计算; x2-1 x2-2x+1 ÷ x+1 x-1 · 1-x x+1 注;分式的混合运算可类比实数进行,同一级的运算应从左到右依次进行,如分式的乘除混合运送,应先把除法统一为乘法,再从左到右计算。 用 科 学 记 数 法 表 示 : — 0.000000108 =__________________(保留 2 个有效数字). 约分:2255xx=_________;122362xx=__________. 9 用科学记数法表示数: 0.000000345 = __________________ .-1.1 10╳-73.45 10╳-7 1 5...